
分析 (1)首先化简二次根式进而合并求出答案;
(2)利用加减消元法解方程组得出答案.
解答 解:(1)原式=2$\sqrt{3}$+3$\sqrt{3}$+$\frac{1}{4}$×4$\sqrt{3}$-15×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$;
(2)解方程组:$\left\{\begin{array}{l}x-y=4,①\\ 2x+y=5.②\end{array}\right.$
①+②得3x=9,x=3.
把x=3代入①得y=-1,
∴原方程组的解是$\left\{\begin{array}{l}x=3\\ y=-1\end{array}\right.$.
点评 此题主要考查了二次根式的加减运算以及二元一次方程组的解法,正确化简二次根式是解题关键.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
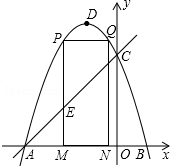 如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
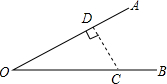 如图,∠O=30°,C为OB上一点,且OC=8,以点C为圆心,半径为4的圆与直线OA的位置关系是( )
如图,∠O=30°,C为OB上一点,且OC=8,以点C为圆心,半径为4的圆与直线OA的位置关系是( )| A. | 相离 | B. | 相交 | ||
| C. | 相切 | D. | 以上三种情况均有可能 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 29.3×107 | B. | 2.93×108 | C. | 0.293×1010 | D. | 2.93×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直角三角形ABC中,∠ACB=90°,AB=15,BC=9,在线段AB上取一点D,作DF⊥AB交AC于点F.现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1,若△E1FA1∽△E1BF,求AD的长.
如图,直角三角形ABC中,∠ACB=90°,AB=15,BC=9,在线段AB上取一点D,作DF⊥AB交AC于点F.现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1,若△E1FA1∽△E1BF,求AD的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com