
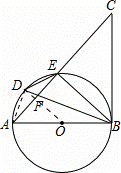
如图,AB是⊙O的直径,点D是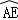 上一点,且∠BDE=∠CBE,BD与AE交于点F.
上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DF•DB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长和⊙O的半径.
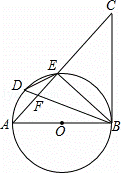
解答: (1)证明:∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠EAB+∠EBA=90°,
∵∠EDB=∠EAB,∠BDE=∠CBE,
∴∠EAB=∠CBE,
∴∠ABE+∠CBE=90°,
∴CB⊥AB,
∵AB是⊙O的直径,
∴BC是⊙O的切线;
(2)证明:∵BD平分∠ABE,
∴∠ABD=∠DBE,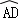 =
=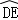 ,
,
∴∠DEA=∠DBE,
∵∠EDB=∠BDE,
∴△DEF∽△DBE,
∴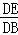 =
=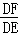 ,
,
∴DE2=DF•DB;
(3)解:连接DA、DO,
∵OD=OB,
∴∠ODB=∠OBD,
∵∠EBD=∠OBD,
∴∠EBD=∠ODB,
∴OD∥BE,
∴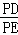 =
=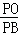 ,
,
∵PA=AO,
∴PA=AO=OB,
∴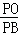 =
=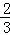
∴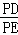 =
=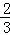 ,
,
∴ =
=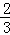 ,
,
∵DE=2,
∴PD=4,
∵∠PDA+∠ADE=180°,∠ABE+∠ADE=180°,
∴∠PDA=∠ABE,
∵OD∥BE,
∴∠AOD=∠ABE,
∴∠PDA=∠AOD,
∵∠P=∠P,
∴△PDA∽△POD,
∴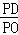 =
=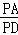 ,
,
设OA=x,
∴PA=x,PO=2x,
∴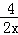 =
=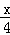 ,
,
∴2x2=16,x=2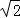 ,
,
∴OA=2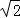 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为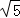 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
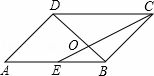
A. m=5 B. m=4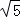 C. m=3
C. m=3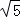 D. m=10
D. m=10
查看答案和解析>>
科目:初中数学 来源: 题型:
学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑比购买3台学习机多600元,购买2台平板电脑和3台学习机共需8400元.
(1)求购买1台平板电脑和1台学习机各需多少元?
(2)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168000元,且购买学习机的台数不超过购买平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣ ;④4ac﹣b2>8a;
;④4ac﹣b2>8a;
其中正确的结论是( )
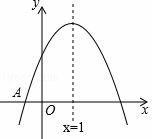
A. ①③④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在边长为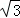 +1的菱形ABCD中,∠A=60°,点E,F分别在AB,AD上,沿EF折叠菱形,使点A落在BC边上的点G处,且EG⊥BD于点M,则EG的长为 .
+1的菱形ABCD中,∠A=60°,点E,F分别在AB,AD上,沿EF折叠菱形,使点A落在BC边上的点G处,且EG⊥BD于点M,则EG的长为 .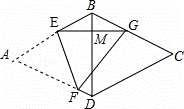
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中, 点A(0,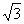 )、B(-1,0),过点A作AB的垂线交
)、B(-1,0),过点A作AB的垂线交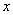 轴于点A1,过点A1作A A1的垂线交
轴于点A1,过点A1作A A1的垂线交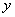 轴于点A2,过点A2作A1A2的垂线交
轴于点A2,过点A2作A1A2的垂线交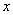 轴于点A3……按此规律继续作下去,直至得到点A2015为止,则点A2015坐标为__________.
轴于点A3……按此规律继续作下去,直至得到点A2015为止,则点A2015坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
某企业开展献爱心扶贫活动,将购买的60吨大米运往贫困地区帮扶贫困居民,现有甲、乙两种货车可以租用.已知一辆甲种货车
和3辆乙种货车一次可运送29吨大米,2辆甲种货车和3辆乙种货车一次可运送37吨大米.
(1)求每辆甲种货车和每辆乙种货车一次分别能装运多少吨大米?
(2)已知甲种货车每辆租金为500元, 乙种货车每辆租金为450元,该企业共租用8辆货车.请求出租用货车的总费用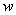 (元)与租用甲种货车的数量
(元)与租用甲种货车的数量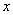 (辆)之间的函数关系式.
(辆)之间的函数关系式.
(3)在(2)的条件下,请你为该企业设计如何租车费用最少?并求出最少费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com