
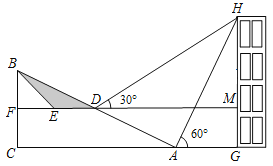
【题目】如图,坡AB的坡度为1:2.4,坡面长26米,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(请将下面两小题的结果都精确到0.1米,参考数据:![]() ≈1.732).
≈1.732).
(1)若修建的斜坡BE的坡角(即∠BEF)恰为45°,则此时平台DE的长为 米;
(2)坡前有一建筑物GH,小明在D点测得建筑物顶部H的仰角为30°,在坡底A点测得建筑物顶部H的仰角为60°,点B、C、A、G、H在同一平面内,点C、A、G在同一条水平直线上,问建筑物GH高为多少米?
【答案】(1)7;(2)建筑物GH高约为17.9米.
【解析】
(1)由勾股定理分别求出BC,AC的长,再证明DF是△ABC的中位线,求出DF、BF的长,即可得出答案;
(2)过点D作DP⊥AC,垂足为P,解直角三角形即可得到结论.
解:(1)∵坡AB的坡度为1:2.4,坡面长26米,
设BC=x米,则AC=2.4x米,
由![]() ,得
,得 ![]()
解得,x=10,或x=-10(舍去)
∴BC=10,AC=24,
∵修建的斜坡BE的坡角∠BEF=45°,D为AB的中点,
∴AD=BD=13,
∵DF//AC,
∴DF为△ABC的中位线,
∴BF=CF=EF=![]() BC=5,DF=
BC=5,DF=![]() AC=12,
AC=12,
故:DE=DF﹣EF=12﹣5=7(米);
则平台DE的长为7m,
故答案为:7;
(2)过点D作DP⊥AC,垂足为P.
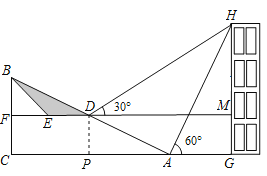
在Rt△DPA中,DP=CF=5,
PA=![]() AC=12,
AC=12,
在矩形DPGM中,MG=DP=12,DM=PG=12+AG,
在Rt△DMH中,
HM=DMtan30°=![]() ×(12+AG),
×(12+AG),
GH=HM+MG=![]() ×(12+AG)+5,
×(12+AG)+5,
∵∠HAG=60°,
∴tan60°=![]() =
=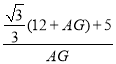 =
=![]() ,
,
解得:AG=![]() ,
,
∴HG=![]() AG=
AG=![]() ≈17.9(米),
≈17.9(米),
答:建筑物GH高约为17.9米.
【点题】
此题主要考查了解直角三角形中坡角问题,根据图象构建直角三角形,进而利用锐角三角函数得出是解题关键.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
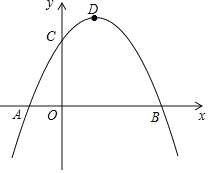
【题目】如图,已知抛物线交x轴于A、B两点,交y轴于C点,A点坐标为(﹣1,0),OC=2,OB=3,点D为抛物线的顶点.
(1)求抛物线的解析式;
(2)P为坐标平面内一点,以B、C、D、P为顶点的四边形是平行四边形,求P点坐标;
(3)若抛物线上有且仅有三个点M1、M2、M3使得△M1BC、△M2BC、△M3BC的面积均为定值S,求出定值S及M1、M2、M3这三个点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受新型冠状病毒肺炎影响,学校开学时间延迟,为了保证学生停课不停学,某校开始实施网上教学,张老师统计了本班学生一周网上上课的时间(单位:分钟)如下:200,180,150,200,250.关于这组数据,下列说法正确的是( )
A.中位数是200B.众数是150C.平均数是190D.方差为0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前,安徽黄山脚下的小村庄的集市上,人山人海,还有人在摆“摸彩”游戏,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1~20号)和1只红球,规定:每次只摸一只球.摸前交1元钱且在1~20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元.
(1)你认为该游戏对“摸彩”者有利吗?说明你的理由.
(2)若一个“摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 在抛物线上,将抛物线
在抛物线上,将抛物线![]() 在点
在点![]() 右侧的部分沿着直线
右侧的部分沿着直线![]() 翻折,翻折后的图象与原抛物线剩余部分合称为图象
翻折,翻折后的图象与原抛物线剩余部分合称为图象![]() .
.
(1)当![]() 时,
时,
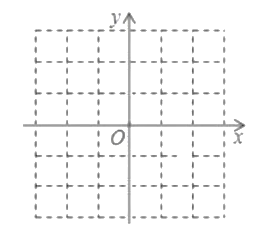
①在如图的平面直角坐标系中画出图象![]() ;
;
②直接写出图象![]() 对应函数的表达式;
对应函数的表达式;
③当![]() 时,图象
时,图象![]() 对应函数的最小值为
对应函数的最小值为![]() 求
求![]() 的取值范围.
的取值范围.
(2)当![]() 时,直接写出图象
时,直接写出图象![]() 对应函数
对应函数![]() 随
随![]() 增大而减小时
增大而减小时![]() 的取值范围.
的取值范围.
(3)若图象![]() 上有且只有三个点到直线
上有且只有三个点到直线![]() 的距离为
的距离为![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于A(-1,n),B(2,-1)两点,与y轴相交于点C.
的图象相交于A(-1,n),B(2,-1)两点,与y轴相交于点C.
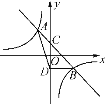
(1)求一次函数与反比例函数的表达式;
(2)若点D与点C关于x轴对称,求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在近期“抗疫”期间,某药店销售![]() 两种型号的口罩,已知销售
两种型号的口罩,已知销售![]() 只
只![]() 型和
型和![]() 只
只![]() 型的利润为
型的利润为![]() 元,销售
元,销售![]() 只
只![]() 型和
型和![]() 只
只![]() 型的利润为
型的利润为![]() 元.
元.
(1)求每只![]() 型口罩和
型口罩和![]() 型口罩的销售利润;
型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共![]() 只,其中
只,其中![]() 型口罩的进货量不超过
型口罩的进货量不超过![]() 型口罩的
型口罩的![]() 倍,设购进
倍,设购进![]() 型口罩
型口罩![]() 只,这
只,这![]() 只口罩的销售总利润为
只口罩的销售总利润为![]() 元.
元.
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②该药店购进![]() 型、
型、![]() 型口罩各多少只,才能使销售总利润最大?
型口罩各多少只,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=
x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=![]() x2+bx+c经过点B,C,与x轴的另一个交点为点A.
x2+bx+c经过点B,C,与x轴的另一个交点为点A.
(1)求抛物线的解析式;
(2)点P是直线BC下方的抛物线上一动点,求四边形ACPB的面积最大时点P的坐标;
(3)若点M是抛物线上一点,请直接写出使∠MBC=![]() ∠ABC的点M的坐标.
∠ABC的点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,延长
,延长![]() 至
至![]() 使
使![]() ,以
,以![]() 为边长在上方作正方形
为边长在上方作正方形![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() 交于点
交于点![]()
![]() .则下列结论:①
.则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )
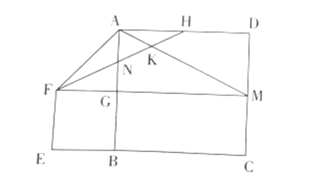
A.①②B.①④C.②③D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com