
【题目】为了测量白塔的高度AB,在D处用高为1.5米的测角仪 CD,测得塔顶A的仰角为42°,再向白塔方向前进12米,又测得白塔的顶端A的仰角为61°,求白塔的高度AB.(参考数据sin42°≈0.67,tan42°≈0.90,sin61°≈0.87,tan61°≈1.80,结果保留整数)
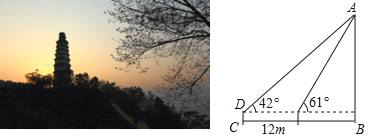
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界最长的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,其中珠海站到香港站全长约55千米,2018年10月24日上午9时正式通车.一辆观光巴士自珠海站出发,25分钟后,一辆小汽车从同一地点出发,结果同时到达香港站.已知小汽车的速度是观光巴士的1.6倍,求观光巴士的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC .
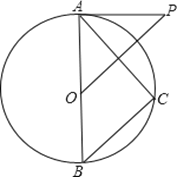
(1)求证:PA为⊙O 的切线;
(2)若OB=5,OP=![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
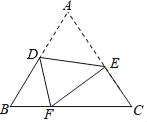
【题目】如图,把等边△ABC沿DE翻折,使点A落在BC上的F处,给出以下结论:
①∠BDF=∠EFC;
②BDCE=BFCF;
③S△BDF+S△EFC=![]() ;
;
④若BF:CF=1:2,则AD:AE=4:5.其中正确的结论有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点B(0,3),点C(4,0)
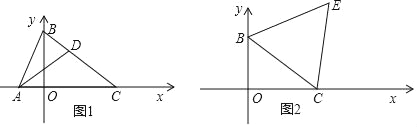
(1)求线段BC的长.
(2)如图1,点A(﹣1,0),D是线段BC上的一点,若△BAD∽△BCA时,求点D的坐标.
(3)如图2,以BC为边在第一象限内作等边△BCE,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱![]() 个,请分别写出从纸箱厂购买纸箱的费用
个,请分别写出从纸箱厂购买纸箱的费用![]() (元)和蔬菜加工厂自己加工制作纸箱的费用
(元)和蔬菜加工厂自己加工制作纸箱的费用![]() (元)关于
(元)关于![]() (个)的函数关系式;
(个)的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.
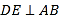
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com