
【题目】毕达哥拉斯学派对”数”与”形”的巧妙结合作了如下研究:
名称及图形 几何点数 层数 | 三角形数 | 正方形数 | 五边形数 | 六边形数 |
|
|
|
| |
第一层几何点数 | 1 | 1 | 1 | 1 |
第二层几何点数 | 2 | 3 | 4 | 5 |
第三层几何点数 | 3 | 5 | 7 | 9 |
… | … | … | … | … |
第六层几何点数 |
|
|
|
|
… | … | … | … | … |
第n层几何点数 |
|
|
|
|
请写出第六层各个图形的几何点数,并归纳出第n层各个图形的几何点数.
【答案】6、11、16、21、n、2n﹣1、3n﹣2、4n﹣3.
【解析】
试题分析:首先看三角形数,根据前三层的几何点数分别是1、2、3,可得第六层的几何点数是6,第n层的几何点数是n;然后看正方形数,根据前三层的几何点数分别是1=2×1﹣1、3=2×2﹣1、5=2×3﹣1,可得第六层的几何点数是2×6﹣1=11,第n层的几何点数是2n﹣1;再看五边形数,根据前三层的几何点数分别是1=3×1﹣2、2=3×2﹣2、3=3×3﹣2,可得第六层的几何点数是3×6﹣2=16,第n层的几何点数是3n﹣2;最后看六边形数,根据前三层的几何点数分别是1=4×1﹣3、5=4×2﹣3、9=4×3﹣3,可得第六层的几何点数是4×6﹣3=21,第n层的几何点数是4n﹣3,据此解答即可.
解:∵前三层三角形的几何点数分别是1、2、3,
∴第六层的几何点数是6,第n层的几何点数是n;
∵前三层正方形的几何点数分别是:1=2×1﹣1、3=2×2﹣1、5=2×3﹣1,
∴第六层的几何点数是:2×6﹣1=11,第n层的几何点数是2n﹣1;
∵前三层五边形的几何点数分别是:1=3×1﹣2、2=3×2﹣2、3=3×3﹣2,
∴第六层的几何点数是:3×6﹣2=16,第n层的几何点数是3n﹣2;
前三层六边形的几何点数分别是:1=4×1﹣3、5=4×2﹣3、9=4×3﹣3,
∴第六层的几何点数是:4×6﹣3=21,第n层的几何点数是4n﹣3.
名称及图形 几何点数 层数 | 三角形数 | 正方形数 | 五边形数 | 六边形数 |
|
|
|
| |
第一层几何点数 | 1 | 1 | 1 | 1 |
第二层几何点数 | 2 | 3 | 4 | 5 |
第三层几何点数 | 3 | 5 | 7 | 9 |
… | … | … | … | … |
第六层几何点数 | 6 | 11 | 16 | 21 |
… | … | … | … | … |
第n层几何点数 | n | 2n﹣1 | 3n﹣2 | 4n﹣3 |
故答案为:6、11、16、21、n、2n﹣1、3n﹣2、4n﹣3.


科目:初中数学 来源: 题型:
【题目】在△ABC中, AB、BC、AC三边的长分别为![]() 、
、![]() 、
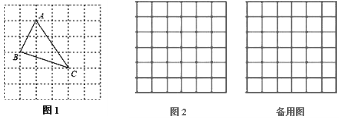
、![]() ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
(1)△ABC的面积为: .
(2)若△DEF三边的长分别为![]() 、
、![]() 、
、![]() ,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.
,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.
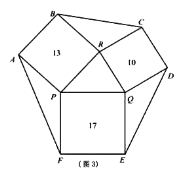
(3)如图3,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13、10、17,请利用第2小题解题方法求六边形花坛ABCDEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,若∠B=60°,则∠1的度数是( )

A.15° B.25° C.10° D.20°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,CA=12![]() cm,BC=12cm;动点P从点C开始沿CA以2
cm,BC=12cm;动点P从点C开始沿CA以2![]() cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BC以 2cm/s的速度向点C移动.如果P、Q、R分别从C、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BC以 2cm/s的速度向点C移动.如果P、Q、R分别从C、A、B同时移动,移动时间为t(0<t<6)s.
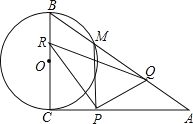
(1)∠CAB的度数是 ;
(2)以CB为直径的⊙O与AB交于点M,当t为何值时,PM与⊙O相切?
(3)写出△PQR的面积S随动点移动时间t的函数关系式,并求S的最小值及相应的t值;
(4)是否存在△APQ为等腰三角形?若存在,求出相应的t值;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某酒店有三人间、双人间客房若干,各种房型每天的收费标准如下:
普通(元/间) | 豪华(元/间) | |
三人间 | 160 | 400 |
双人间 | 140 | 300 |
一个50人的旅游团到该酒店入住,选择了一些三人普通间和双人豪华间入住,且恰好住满.已知该旅游团当日住宿费用共计4020元,问该旅游团入住的三人普通间和双人豪华间各为几间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(﹣10,0),B(﹣6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(8,0)出发,沿x轴向左以每秒1个单位长的速度向点A匀速运动,运动时间为t秒.
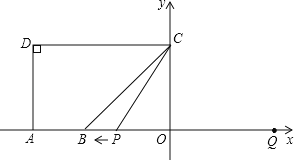
(1)求点C的坐标;
(2)当∠BCP=15°,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
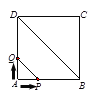
【题目】如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间的函数关系可用图象表示为 ( )
A. 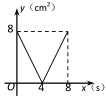 B.
B. 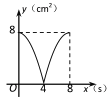 C.
C. 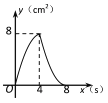 D.
D. 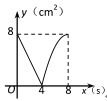
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 全等三角形的高相等 B. 全等三角形的中线相等
C. 全等三角形的角平分线相等 D. 全等三角形的对应角平分线相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com