练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】阅读材料：求l+2+22+23+24+…+22013的值．

    解：设S=l+2+22+23+24+…+22012+22013，将等式两边同时乘2，

    得2S=2+22+23+24+25+…+22013+22014． 将下式减去上式，得2S﹣S=22014－1

    即S=22014－1，

    即1+2+22+23+24+…+22013=22014－1

    仿照此法计算：（1）1+3+32+33+…+3100；（2）1++++…+，

    【答案】（1）；（2）

    【解析】解：（1）设S=1+3+32+33+…+3100，

    两边乘以3得：3S=3+32+33+34+35+…+3100+3101，

    将下式减去上式，得3S﹣S=3101﹣l

    即S=，

    即1+3+32+33+34+…+3100=

    （2）设S=1++++…+，

    两边乘以得： S=++，

    将下式减去上式得：﹣ S=﹣1，

    解得：S=2﹣，

    即1++++…+=2﹣．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=x2﹣x﹣1与x轴的一个交点为（m，0），则代数式m2﹣m﹣2009的值为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列数据不能用有序数对表示的是( )

    A. 4楼，5楼 B. 6楼，8号 C. 3号路，25号 D. 东经110°，北纬67°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各组数中，不能成为直角三角形的三条边长的是（　　）

    A. 3，4，5B. 7，24，25C. 6，8，10D. 9，11，13

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一元二次方程ax2﹣bx﹣2018=0有一个根为x=﹣1，则a+b=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】据统计，2014年全国约有939万人参加高考，939万人用科学记数法表示为____________人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果一个实数的算术平方根等于它的立方根，那么满足条件的实数有( )

    A. 0个 B. 1个 C. 2个 D. 3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，D是AB上一点，且∠ACD=∠B．

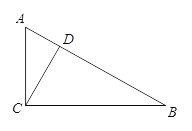
    （1）求证：CD⊥AB；

    （2）在（1）中画△ABC的角平分线AE，交CD于点F，试判断∠AEC与∠CFE的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，对于任意三点， ， 的“矩面积”，给出如下定义：任意两点横坐标差的最大值称为“水平底”，任意两点纵坐标差的最大值称为“铅垂高”，“水平底”与“铅垂高”的乘积为点， ， 的“矩面积”，即“矩面积”.

    例如：点， ， ，它们的“水平底”，“铅垂高”，“矩面积”.

    （1）已知点， ， .

    ①若， ， 三点的 “矩面积”为12，写出点的坐标： ；

    ②写出， ， img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/28/23/79963a76/SYS201712282330522238895478_ST/SYS201712282330522238895478_ST.027.png" width="16" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />三点的“矩面积”的最小值： .

    （2）已知点， ， ，

    ①当D，E，F三点的“矩面积”取最小值时，写出的取值范围： ；

    ②若D，E，F三点的“矩面积”为33，求点的坐标；

    ③设D，E，F三点的“矩面积”为，写出与t的函数关系式.

    查看答案和解析>>

    同步练习册答案