
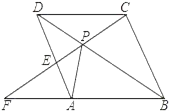
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
(1)图中△APD与哪个三角形全等:_____.
(2)猜想:线段PC、PE、PF之间存在什么关系:_____.
【答案】(1)△APD≌△CPD(SAS);(2) PC2=PEPF.
【解析】
(1)根据菱形的性质得∠ADP=∠CDP,DA=DC,从而得到△APD与△CPD全等.
(2)根据菱形的对边互相平行得∠DCF=∠F,再根据(1)题的结论得到∠DCP=∠DAP,从而证得△PAE∽△PFA,然后利用比例线段证得等积式即可.
(1)∵四边形ABCD为菱形,
∴∠ADP=∠CDP,DC=DA,
在△APD和△CPD中,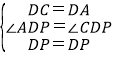 ,
,
∴△APD≌△CPD(SAS);
(2)∵四边形ABCD为菱形,
∴∠DCF=∠F,
∵△APD≌△CPD,
∴∠DCP=∠DAP,
∴∠F=∠PAE,
∠APE=∠FPA
∴△PAE∽△PFA,
∴![]() ,
,
即:PA2=PEPF,
∵P是菱形ABCD的对角线BD上一点,
∴PA=PC,
∴PC2=PEPF.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
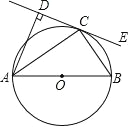
【题目】如图,AB 为⊙O 的直径,C 为⊙O 上一点,AD⊥CE 于点 D,AC 平分∠DAB.
(1) 求证:直线 CE 是⊙O 的切线;
(2) 若 AB=10,CD=4,求 BC 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,点P在BC上.若点P为BC的中点,则m=AP2+BPPC的值为多少?若BC边上有100个不同的点P1,P2,…,P100,且mi=APi2+BPiPiC(i=1,2,…,100),则m=m1+m2+…+m100 的值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
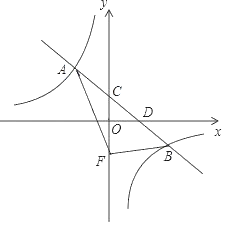
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y=![]() (k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式﹣![]() x+b>
x+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为![]() .
.
(1)求k的值;
(2)若双曲线y=![]() 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=![]() 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
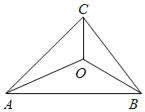
【题目】如图,已知等腰三角形ABC,CA=CB=6cm,AB=8cm,点O为△ABC内一点(点O不在△ABC边界上).请你运用图形旋转和“两点之间线段最短”等数学知识、方法,求出OA+OB+OC的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定:转动两个转盘停止后,指针必须指到某一数字,否则重转.
(1)请用树状图或列表法列出所有可能的结果;
(2)若指针所指的两个数字都是方程x2-5x+6=0的解时,则甲获胜;若指针所指的两个数字都不是方程x2-5x+6=0的解时,则乙获胜,问他们两人谁获胜的概率大?请分析说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
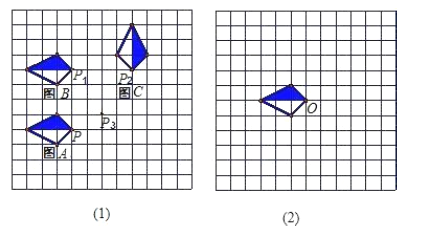
【题目】(1)如图(1),在方格纸中如何通过平移或旋转这两种变换,由图形![]() 得到图形
得到图形![]() ,再由图形
,再由图形![]() 得到图形
得到图形![]() ?
?
(2)如图(1),如果点![]() 、点
、点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,写出点
,写出点![]() 的坐标;
的坐标;
(3)如图(2)所示是某设计师设计的图案的一部分,请你运用旋转变换的方法,在方格纸中将图形绕点![]() 顺时针依次旋转
顺时针依次旋转![]() 、
、![]() 、
、![]() ,依次画出旋转后得到的图形.
,依次画出旋转后得到的图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com