
【题目】在下列括号内填理由:已知:如图,AC∥DE,CD、EF分别为∠ACB、∠DEB的平分线.
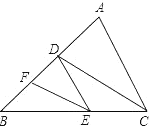
求证:CD∥EF
证明:∵AC∥DE〔已知)
∴ = ( )
∵CD、EF分别为∠ACB、∠DEB的平分线.(已知)
![]() ,
,![]() ( )
( )
∴∠DCB=∠FEB
∴CD∥EF( )
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系 xOy 中,A(2,3),B(3,1),C(﹣2,﹣1).
①在图中作出△ABC 关于 x 轴的对称图形△A1B1C1 并写出 A1,B1,C1 的坐标;
②在 y 轴上画出点 P,使 PA+PB 最小.(不写作法,保留作图痕迹)
③求△ABC 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠BCA=90°,BC=AC,直角顶点C在y轴上,锐角顶点A在x轴上.
(1)如图①,若点C的坐标是(0,-1),点A的坐标是(-3,0),求B点的坐标;
(2)如图②,若x轴恰好平分∠BAC,BC与x轴交于点D,过点B作BE⊥x轴于E,问AD与BE有怎样的数量关系,并说明理由;
(3)如图③,直角边AC在两坐标轴上滑动,使点B在第四象限内,过B点作BF⊥x轴于F,在滑动的过程中,猜想OC、BF、OA之间的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)求△ABC的面积为_______;
(3)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,M是AB上的动点
,M是AB上的动点![]() 不与A、B重合
不与A、B重合![]() ,过点M作
,过点M作![]() 交AC于点N,以MN为直径作
交AC于点N,以MN为直径作![]() ,并在
,并在![]() 内作内接矩形
内作内接矩形![]() 设
设![]() .
.
![]() 的面积
的面积![]() ______,
______,![]() ______;
______;![]() 用含x的代数式表示
用含x的代数式表示![]()
![]() 在动点M的运动过程中,设
在动点M的运动过程中,设![]() 与四边形MNCB重合部分的面积为
与四边形MNCB重合部分的面积为![]() 试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?
试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB于点D,点E在CD上,下列四个条件:①AD=ED;②∠A=∠BED;③∠C=∠B;④AC=EB,将其中两个作为条件,不能判定△ADC≌△EDB的是

A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举办了绿色阅读节活动,为了表彰优秀,陈老师负责购买奖品,在购买时他发现身上所带的钱:若以2支钢笔和3个笔记本为一份奖品,则可买50份奖品;若以2支钢笔和6本笔记本为一份奖品,则可以买40份奖品,设钢笔单价为![]() 元/支,笔记本单价为
元/支,笔记本单价为![]() 元/支.
元/支.
(1)请用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)若用这笔钱全部购买笔记本,总共可以买几本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com