
【题目】如图,在正方形![]() 中,点E是对角线
中,点E是对角线![]() 上一点,连接
上一点,连接![]() .过点E作
.过点E作![]() 交
交![]() 的延长线于点F.若
的延长线于点F.若![]() ,
,![]() ,则正方形
,则正方形![]() 的面积为______.
的面积为______.

【答案】16
【解析】
由∠EHC=∠BHF,∠CEH=∠FBH=90°可判定△ECH∽△BFH,从而得到∠ECH=∠BFH;作辅助线可证明四边形ENBM是正方形,根据正方形的性质得EM=EN,由角角边可证明△ENC≌△EMF,得CN=FM;因![]() ,可求MB的长度,从而求得CN和BC的长,可求出正方形ABCD的面积.
,可求MB的长度,从而求得CN和BC的长,可求出正方形ABCD的面积.
解:过点E作EN⊥BC,EM⊥AB,分别交BC、AB于N、M两点,
且EF与BC相交于点H.
∵EF⊥CE,∠ABC=90°,∠ABC+∠HBF=180°,
∴∠CEH=∠FBH=90°,
又∵∠EHC=∠BHF,
∴△ECH∽△BFH(AA),
∴∠ECH=∠BFH,
∵EN⊥BC,EM⊥AB,四边形ABCD是正方形,
∴四边形ENBM是正方形,
∴EM=EN,∠ENC=∠EMF=90°,
在△ENC和△EMF中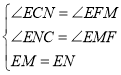
∴△ENC≌△EMF(AAS)
∴CN=FM,
又∵在正方形ENBM中,![]()
∴MB=BN=1,
∵BF=2
∴MF=CN=1+2=3
∴BC=4
∴正方形ABCD的面积为16
故答案为:16.


科目:初中数学 来源: 题型:
【题目】如图所示,在直角坐标系中,已知![]() 、
、![]() 、
、![]() 三点,其中
三点,其中![]() 、
、![]() 、
、![]() 满足关系式
满足关系式![]() ,
, ![]() ≤
≤![]() .
.
(1)![]() =_______;
=_______; ![]() =________;
=________; ![]() =_______.
=_______.
(2)如果点![]() 是第二象限内的一个动点,坐标为
是第二象限内的一个动点,坐标为![]() .将四边形
.将四边形![]() 的面积用
的面积用![]() 表示,请你写出
表示,请你写出![]() 关于
关于![]() 的函数表达式,并写出自变量的取值范围.
的函数表达式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点![]() ,使得四边形的面积
,使得四边形的面积![]() 与
与![]() 的面积相等?若存在,请求出点
的面积相等?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
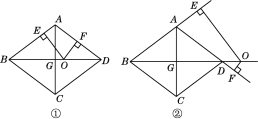
【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)求对角线AC的长及菱形ABCD的面积.
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】食品安全关乎民生,食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存.某饮料厂为了解A、B两种饮料添加剂的添加情况,随机抽检了A种30瓶,B种70瓶,检测发现,A种每瓶比B种每瓶少1克添加剂,两种共加入了添加剂270克,求A、B两种饮料每瓶各加入添加剂多少克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线l:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交l于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3,…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…,则S8等于( )

A.28B.213C.216D.218
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为BC上一点,BE=2CE,连接DE,F为DE中点,以DF为直角边作等腰Rt△DFG,连接BG,将△DFG绕点D顺时针旋转得△DF′G′,G′恰好落在BG的延长线上,连接F′G,若BG=2![]() ,则S△GF′G′=________.
,则S△GF′G′=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为方便市民通行,某广场计划对坡角为30°,坡长为60 米的斜坡AB进行改造,在斜坡中点D 处挖去部分坡体(阴影表示),修建一个平行于水平线CA 的平台DE 和一条新的斜坡BE.

(1)若修建的斜坡BE 的坡角为36°,则平台DE的长约为多少米?
(2)在距离坡角A点27米远的G处是商场主楼,小明在D点测得主楼顶部H 的仰角为30°,那么主楼GH高约为多少米?
(结果取整数,参考数据:sin 36°=0.6,cos 36°=0.8,tan 36°=0.7,![]() =1.7)
=1.7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com