
【题目】如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.

(1)求证:四边形ABEF是正方形;
(2)如果AB=6,AD=8,求tan∠ADP的值.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)由矩形的性质得出∠FAB=∠ABE=90°,AF∥BE,证出四边形ABEF是矩形,再证明AB=BE,即可得出四边形ABEF是正方形;
(2)由正方形的性质得出BP=PF,BA⊥AD,∠PAF=45°,得出AB∥PH,求出DH=AD-AH=5,在Rt△PHD中,由三角函数即可得出结果.
试题解析:
(1)证明:∵四边形ABCD是矩形,
∴∠FAB=∠ABE=90°,AF∥BE,
∵EF⊥AD,
∴∠FAB=∠ABE=∠AFE=90°,
∴四边形ABEF是矩形,
∵AE平分∠BAD,AF∥BE,
∴∠FAE=∠BAE=∠AEB,
∴AB=BE,
∴四边形ABEF是正方形;
(2)解:过点P作PH⊥AD于H,如图所示:
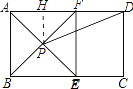
∵四边形ABEF是正方形,
∴BP=PF,BA⊥AD,∠PAF=45°,
∴AB∥PH,
∵AB=6,
∴AH=PH=3,
∵AD=8,
∴DH=AD﹣AH=8﹣3=5,
在Rt△PHD中,∠PHD=90°.
∴tan∠ADP= ![]() =
= ![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中 ,AB=8 , BC=6, 点P在边AB上。若将△DAP沿DP折叠 ,使点A落在矩形对角线上的点A,处,则AP的长为__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地在进入防汛期间,准备对4800米长的河堤进行加固,在加固工程中,该地驻军出色地完成了任务,它们在加固600米后,采用了新的加固模式,每天加固的长度是原来的2倍,结果只用9天就完成了加固任务.
(1)求该地驻军原来每天加固大坝的米数;
(2)由于汛情严重,该驻军部队又接到了加固一段长4200米大坝的任务,他们以上述新的加固模式进行了2天后,接到命令,必须在4天内完成剩余任务,求该驻军每天至少还要再多加固多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正△ABC与正六边形DEFGH的边长相等,初始如图所示,将三角形绕点I顺时针旋转使得AC与CD重合,再将三角形绕点D顺时针旋转使得AB与DE重合,…,按这样的方式将△ABC旋转2015次后,△ABC中与正六边形DEFGHI重合的边是( )

A. AB B. BC C. AC D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AE平分∠BAD,交BC于E,DE⊥AE,下列结论::①DE平分∠ADC;②E是BC的中点;③AD=2CD;④梯形ADCE的面积与△ABE的面积比是3:1,其中正确的结论的个数有( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线AC的解析式为y=﹣![]() x+1,直线AC交x轴于点C,交y轴于点A.
x+1,直线AC交x轴于点C,交y轴于点A.
(1)若等边△OBD的顶点D与点C重合,另一顶点B在第一象限内,直接写出点B的坐标;
(2)过点B作x轴的垂线l,在l上是否存在一点P,使得△AOP的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)试在直线AC上求出到两坐标轴距离相等的所有点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
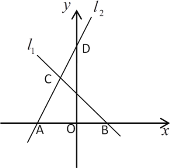
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() (0,5),与直线
(0,5),与直线![]() 交于点
交于点![]() (﹣1,
(﹣1,![]() ),且与
),且与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
(2)求△![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +8 |
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com