
����Ŀ��ij���½���Բ���Ļ��㳡��С�ܺ�С������ͬ�ķ��������ù㳡�İ뾶.
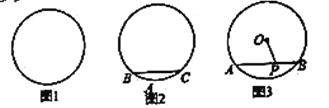
��1��С������Բ�ģ������뾶��������ͼ1�У��ó߹���ͼ�ķ�����С���ҵ��ù㳡��Բ��![]() ����д������������ͼ�ۼ�����
����д������������ͼ�ۼ�����
��2��С���ڹ㳡�ߣ���ͼ2��ѡȡ![]() ��
��![]() ��
��![]() ����ʯ��������
����ʯ��������![]() ��
��![]() ֮��ľ�����
֮��ľ�����![]() ��
��![]() ֮��ľ�����ȣ������
֮��ľ�����ȣ������![]() ��Ϊ240�ף�
��Ϊ240�ף�![]() ��
��![]() �ľ���Ϊ5��.�����������㳡�İ뾶��
�ľ���Ϊ5��.�����������㳡�İ뾶��
��3����������������⣺��ͼ3��![]() ��ֱ��Ϊ
��ֱ��Ϊ![]() ����
����![]() ��
��![]() ����
����![]() �ϵ�һ�����㣬���
�ϵ�һ�����㣬���![]() �ij��ȷ�Χ�Ƕ��٣�
�ij��ȷ�Χ�Ƕ��٣�
���𰸡���1�������������2���㳡�İ뾶1443�ף���3��![]() .
.
��������
��1�������ҵĴ�ֱƽ���ߣ��ٽ�ϴ����������۵ó�Բ��λ�ã�
��2����Բ��ΪO������ OA��OB��OA��BC��D������A��B֮��ľ�����A��C֮��ľ�����ȣ��ó�![]() ���Ӷ��ó�BD=DC=
���Ӷ��ó�BD=DC=![]() BC���ٸ��ݹ��ɶ����ó�OB2=OD2+BD2����OB=x����������㳡�İ뾶��
BC���ٸ��ݹ��ɶ����ó�OB2=OD2+BD2����OB=x����������㳡�İ뾶��
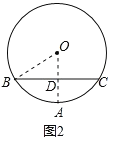
��3������O��OE��AB�ڵ�E������OB���ɴ���������֪AE=BE=![]() AB���ٸ��ݹ��ɶ������OE�ij����ɴ˿ɵó����ۣ�
AB���ٸ��ݹ��ɶ������OE�ij����ɴ˿ɵó����ۣ�
�⣺��ͼ1��ʾ����Բ��������2���ҵĴ�ֱƽ���ߣ��ɴ���������֪��2����ֱƽ���߱ض���Բ��2��ֱ���غϣ����Խ���![]() ��Ϊ����
������
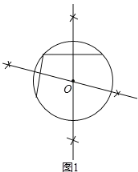
��2����ͼ2������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ���ף���
���ף���
������![]() ��
��
��![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
��ã�![]() ��
��
![]() ��
��
��㳡�İ뾶1443��.
��3����ͼ3������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��ֱ��Ϊ
��ֱ��Ϊ![]() ��
��
��![]() ��
��
��![]() ��
��
�ߴ��߶���̣��뾶���
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������� ![]() ��7��ֵ�Ƕ��κ���
��7��ֵ�Ƕ��κ���![]() ͼ���ϵĵ�����Ӧ�����꣬����
ͼ���ϵĵ�����Ӧ�����꣬���� ![]()
x | �� |
|
|
|
|
|
|
| �� |
y | �� | 7 | m | 14 | k | 14 | m | 7 | �� |
���ݱ����ṩ����Ϣ��������4 ���жϣ�
�� ![]() ����
���� ![]() ���� ��
���� ��![]() ʱ��y ��ֵ�� k����
ʱ��y ��ֵ�� k���� ![]() �����ж���ȷ���� �� ��
�����ж���ȷ���� �� ��
A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
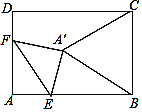
����Ŀ����ͼ���ھ���ABCD�У�AB=8��AD=6����EΪAB��һ�㣬AE=2![]() ����F��AD�ϣ�����AEF��EF�۵������۵����A�Ķ�Ӧ��A��ǡ������BC�Ĵ�ֱƽ������ʱ���ۺ�EF�ij�Ϊ_____��
����F��AD�ϣ�����AEF��EF�۵������۵����A�Ķ�Ӧ��A��ǡ������BC�Ĵ�ֱƽ������ʱ���ۺ�EF�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��ͼ���㣨��1��4��������ֱ��
��ͼ���㣨��1��4��������ֱ��![]() �ཻ��A��B���㣨��ͼ����A����y���ϣ�����B��BC��x�ᣬ����Ϊ��C����3��0����
�ཻ��A��B���㣨��ͼ����A����y���ϣ�����B��BC��x�ᣬ����Ϊ��C����3��0����
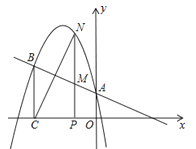
��1������κ����ı���ʽ��
��2����N�Ƕ��κ���ͼ����һ�㣨��N��AB�Ϸ�������N��NP��x�ᣬ����Ϊ��P����AB�ڵ�M����MN�����ֵ��
��3���ڣ�2���������£���N�ں�λ��ʱ��BM��NC���ֱƽ�֣��������������������N������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
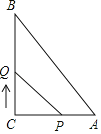
����Ŀ����ͼ���ڡ�ABC�У���C��90�㣬AC��6cm��BC��8cm����P�ӵ�A������AC��1cm/s���ٶ����C�ƶ���ͬʱ��Q��C�������CB��2cm/s���ٶ����B�ƶ�����Q�˶���B��ʱ��P��Qֹͣ�˶������P�˶���ʱ��Ϊts��
��1��tΪ��ֵʱ����PCQ���������5cm2��
��2����P��Q���ƶ������У��Ƿ����ijһʱ�̣�ʹ�á�PCQ��������ڡ�ABC�������һ�룿�����ڣ����t��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���ڴ���װ�Űס��졢��������ɫ��С����ɫ����״��С��ȫ��ͬ�������а���3��������2��������1����
��1������Ӵ���ȡ��һ������ȡ�������Ǻ���ĸ��ʣ�
��2����ȡ���ĵ�һֻ���Ǻ��������Żش���Ӵ������µ������������ȡ��1������ʱȡ�������Ǻ���ĸ����Ƕ��٣�
��3����ȡ��һ�������Żش��У��Ӵ����������ȡ��һ��������ȡ�������ǰ���ĸ����Ƕ��٣������б�������״ͼ���㣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ��
�ύ��![]() ����(
����(![]() ��
��![]() �����)����
�����)����![]() �ύ�ڵ�
�ύ�ڵ�![]() �� ��
�� ��![]() ���
���![]() ���������ߵĶԳ���Գ�.
���������ߵĶԳ���Գ�.
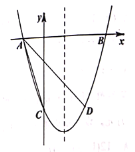
(1)�������ߵĽ���ʽ����![]() ������:
������:
(2)��![]() �������߶Գ����ϵ�һ���㣬��
�������߶Գ����ϵ�һ���㣬��![]() ���ܳ���Сʱ�������
���ܳ���Сʱ�������![]() ������;
������;
(3)��![]() ��
��![]() ���ϣ���
���ϣ���![]() ����ֱ��д����
����ֱ��д����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У��Խ���AC��BD�ཻ�ڵ�O����DC���ӳ�����ȡһ��E������OE��BC�ڵ�F����֪AB=4��BC=6��CE=2����CF�ij����ڣ� ��

A. 1 B. 1.5 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=AC����E��F�ֱ�Ϊ��AB��BC�ϵĵ㣬��AE=BF������CE��AF���ڵ�H�������н��ۣ��١�ABF�ա�CAE���ڡ�AHC=120�㣻�ۡ�AEH�ס�CEA����AEAD=AHAF�����н�����ȷ�ĸ������� ��
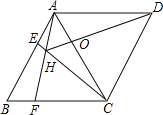
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com