
【题目】如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2![]() ,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为_____.
,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为_____.
【答案】4或4![]() .
.
【解析】
①当AF<![]() AD时,由折叠的性质得到A′E=AE=2
AD时,由折叠的性质得到A′E=AE=2![]() ,AF=A′F,∠FA′E=∠A=90°,过E作EH⊥MN于H,由矩形的性质得到MH=AE=2
,AF=A′F,∠FA′E=∠A=90°,过E作EH⊥MN于H,由矩形的性质得到MH=AE=2![]() ,根据勾股定理得到A′H=
,根据勾股定理得到A′H=![]() ,根据勾股定理列方程即可得到结论;②当AF>
,根据勾股定理列方程即可得到结论;②当AF>![]() AD时,由折叠的性质得到A′E=AE=2
AD时,由折叠的性质得到A′E=AE=2![]() ,AF=A′F,∠FA′E=∠A=90°,过A′作HG∥BC交AB于G,交CD于H,根据矩形的性质得到DH=AG,HG=AD=6,根据勾股定理即可得到结论.
,AF=A′F,∠FA′E=∠A=90°,过A′作HG∥BC交AB于G,交CD于H,根据矩形的性质得到DH=AG,HG=AD=6,根据勾股定理即可得到结论.
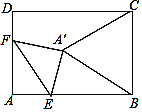
①当AF<![]() AD时,如图1,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上,
AD时,如图1,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上,

则A′E=AE=2![]() ,AF=A′F,∠FA′E=∠A=90°,
,AF=A′F,∠FA′E=∠A=90°,
设MN是BC的垂直平分线,
则AM=![]() AD=3,
AD=3,
过E作EH⊥MN于H,
则四边形AEHM是矩形,
∴MH=AE=2![]() ,
,
∵A′H=![]() ,
,
∴A′M=![]() ,
,
∵MF2+A′M2=A′F2,
∴(3-AF)2+(![]() )2=AF2,
)2=AF2,
∴AF=2,
∴EF=![]() =4;
=4;
②当AF>![]() AD时,如图2,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上,
AD时,如图2,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上,
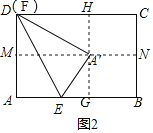
则A′E=AE=2![]() ,AF=A′F,∠FA′E=∠A=90°,
,AF=A′F,∠FA′E=∠A=90°,
设MN是BC的垂直平分线,
过A′作HG∥BC交AB于G,交CD于H,
则四边形AGHD是矩形,
∴DH=AG,HG=AD=6,
∴A′H=A′G=![]() HG=3,
HG=3,
∴EG=![]() =
=![]() ,
,
∴DH=AG=AE+EG=3![]() ,
,
∴A′F=![]() =6,
=6,
∴EF=![]() =4
=4![]() ,
,
综上所述,折痕EF的长为4或4![]() ,
,
故答案为:4或4![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
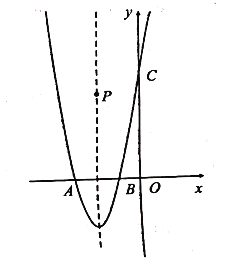
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() ,点
,点![]() 的坐标;
的坐标;
(2)我们规定:对于直线![]() ,直线
,直线![]() ,若
,若![]() ,则直线
,则直线![]() ;反过来也成立.请根据这个规定解决下列问题:
;反过来也成立.请根据这个规定解决下列问题:
①直线![]() 与直线
与直线![]() 是否垂直?并说明理由;
是否垂直?并说明理由;
②若点![]() 是抛物线
是抛物线![]() 的对称轴上一动点,是否存在点
的对称轴上一动点,是否存在点![]() 与点
与点![]() ,点
,点![]() 构成以
构成以![]() 为直角边的直角三角形?若存在,请求出点
为直角边的直角三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
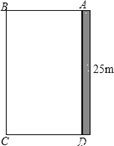
【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带的BC边长为x m,绿化带的面积为y m2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,满足条件的绿化带的面积最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E、F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动,设运动时间为t秒(t>0).
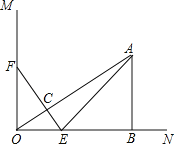
(1)当t=1秒时,△EOF与△ABO是否相似?请说明理由;
(2)在运动过程中,不论t取何值,总有EF⊥OA,为什么?
(3)在运动过程中,是否存在某一时刻t,使得△AEB与△OEF相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司共有汽车50辆,市场调查表明,当租金为每辆每日200元时可全部租出,当租金每提高10元,租出去的车就减少2辆.
(1)当租金提高多少元时,公司的每日收益可达到10120元?
(2)公司领导希望日收益达到10200元,你认为能否实现?若能,求出此时的租金,若不能,请说明理由.
(3)汽车日常维护要一定费用,已知外租车辆每日维护费为100元,未租出的车辆维护费为50元,当租金为多少元时,公司的利润恰好为5500元?(利润=收益一维护费).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 的对称轴为
的对称轴为![]() ,且经过点A(2,1),点
,且经过点A(2,1),点![]() 是抛物线上的动点,
是抛物线上的动点,![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,
,![]() ,过点A作AE⊥x轴,垂足为E.则当
,过点A作AE⊥x轴,垂足为E.则当![]() ( )时,
( )时,![]() 的周长最小.
的周长最小.
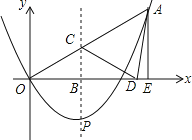
A.1B.1.5C.2D.2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市新建了圆形文化广场,小杰和小浩准备不同的方法测量该广场的半径.
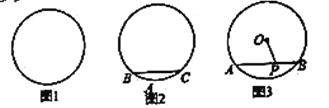
(1)小杰先找圆心,再量半径,请你在图1中,用尺规作图的方法帮小杰找到该广场的圆心![]() (不写作法,保留作图痕迹);
(不写作法,保留作图痕迹);
(2)小浩在广场边(如图2)选取![]() 、
、![]() 、
、![]() 三根石柱,量得
三根石柱,量得![]() 、
、![]() 之间的距离与
之间的距离与![]() 、
、![]() 之间的距离相等,并测得
之间的距离相等,并测得![]() 长为240米,
长为240米,![]() 到
到![]() 的距离为5米.请你帮他求出广场的半径;
的距离为5米.请你帮他求出广场的半径;
(3)请你解决下面的问题:如图3,![]() 的直径为
的直径为![]() ,弦
,弦![]() ,
,![]() 是弦
是弦![]() 上的一个动点,求出
上的一个动点,求出![]() 的长度范围是多少?
的长度范围是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
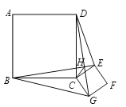
【题目】如图,正方形ABCD和正方形CEFG的边长分别为a和b,BE和DG相交于点H,连接HC,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确的结论是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com