
【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带的BC边长为x m,绿化带的面积为y m2.
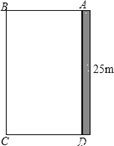
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,满足条件的绿化带的面积最大.
科目:初中数学 来源: 题型:
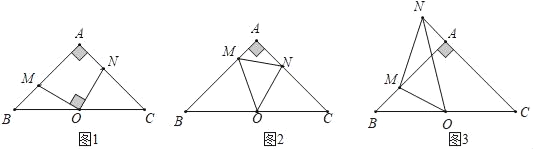
【题目】在Rt△ABC中,AB=AC,OB=OC,∠A=90°,∠MON=α,分别交直线AB、AC于点M、N.
(1)如图1,当α=90°时,求证:AM=CN;
(2)如图2,当α=45°时,问线段BM、MN、AN之间有何数量关系,并证明;
(3)如图3,当α=45°时,旋转∠MON,问线段之间BM、MN、AN有何数量关系?并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】表中所列 ![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中 ![]()
x | … |
|
|
|
|
|
|
| … |
y | … | 7 | m | 14 | k | 14 | m | 7 | … |
根据表中提供的信息,有以下4 个判断:
① ![]() ;②
;② ![]() ;③ 当
;③ 当![]() 时,y 的值是 k;④
时,y 的值是 k;④ ![]() 其中判断正确的是 ( )
其中判断正确的是 ( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O是△ABC的外接圆,点D是![]() 上一动点(不与点A、C重合),且∠ADB=∠BAC=45°.
上一动点(不与点A、C重合),且∠ADB=∠BAC=45°.
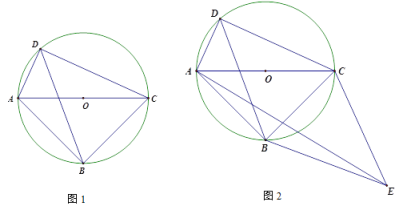
(1)求证:AC是⊙O的直径;
(2)当点D在![]() 运动到使AD+CD=5
运动到使AD+CD=5![]() 时,则线段BD的长为 ;(直接写出结果)
时,则线段BD的长为 ;(直接写出结果)
(3)如图2,把△DBC沿直线BC翻折得到△EBC,连接AE,当点D在![]() 运动时,探究线段AE、BD、CD之间的数量关系,并说明理由.
运动时,探究线段AE、BD、CD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
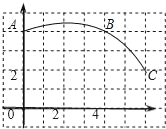
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,则⊙D的半径为 ;扇形DAC的圆心角度数为 ;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
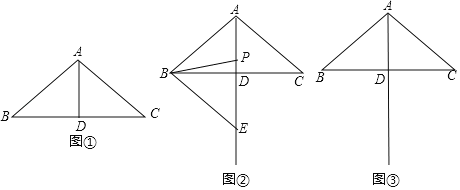
【题目】如图①,在△ABC中,AB=AC=3,∠BAC=100°,D是BC的中点.
小明对图①进行了如下探究:在线段AD上任取一点P,连接PB.将线段PB绕点P按逆时针方向旋转80°,点B的对应点是点E,连接BE,得到△BPE.小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.
请你帮助小明继续探究,并解答下列问题:
(1)当点E在直线AD上时,如图②所示.
①∠BEP= °;
②连接CE,直线CE与直线AB的位置关系是 .
(2)请在图③中画出△BPE,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
(3)当点P在线段AD上运动时,求AE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
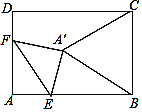
【题目】如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2![]() ,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为_____.
,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
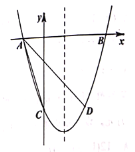
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() , 点
, 点![]() 与点
与点![]() 关于抛物线的对称轴对称.
关于抛物线的对称轴对称.
(1)求抛物线的解析式及点![]() 的坐标:
的坐标:
(2)点![]() 是抛物线对称轴上的一动点,当
是抛物线对称轴上的一动点,当![]() 的周长最小时,求出点
的周长最小时,求出点![]() 的坐标;
的坐标;
(3)点![]() 在
在![]() 轴上,且
轴上,且![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com