
【题目】如图1,⊙O是△ABC的外接圆,点D是![]() 上一动点(不与点A、C重合),且∠ADB=∠BAC=45°.
上一动点(不与点A、C重合),且∠ADB=∠BAC=45°.
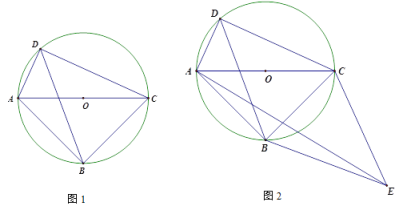
(1)求证:AC是⊙O的直径;
(2)当点D在![]() 运动到使AD+CD=5
运动到使AD+CD=5![]() 时,则线段BD的长为 ;(直接写出结果)
时,则线段BD的长为 ;(直接写出结果)
(3)如图2,把△DBC沿直线BC翻折得到△EBC,连接AE,当点D在![]() 运动时,探究线段AE、BD、CD之间的数量关系,并说明理由.
运动时,探究线段AE、BD、CD之间的数量关系,并说明理由.
【答案】(1)见解析;(2)5;(3)AE2=2BD2+CD2,理由见解析.
【解析】
(1)根据圆周角定理,可得∠BDC=∠BAC=45°,可求出∠ADC=90°根据圆周角定理的推论可得结论;
(2)作AM⊥BD于M,CN⊥BD于N,由等腰直角三角形的性质得AD=![]() DM,CE=
DM,CE=![]() DN,证△ABM≌△BCN,可得BN=AM=DM,即可得出BD=BN+DN,从而求得BD的长;
DN,证△ABM≌△BCN,可得BN=AM=DM,即可得出BD=BN+DN,从而求得BD的长;
(3)延长DA到点F,使得AF=CD,连接BF,由(2)得BD=![]() (AD+CD)=
(AD+CD)=![]() DF,可得△BDF为等腰直角三角形,则BF=BD,DF2=2BD2,连接CF,证△CBF≌△ABE,可得AE=CF,在Rt△FDC中,CF2=DF2+CD2,即AE2=2BD2+CD2.
DF,可得△BDF为等腰直角三角形,则BF=BD,DF2=2BD2,连接CF,证△CBF≌△ABE,可得AE=CF,在Rt△FDC中,CF2=DF2+CD2,即AE2=2BD2+CD2.
(1)证明:∵∠BDC、∠BAC都是![]() 所对的圆周角,∠BAC=45°
所对的圆周角,∠BAC=45°
∴∠BDC=∠BAC=45°
∵∠ADB=45°
∴∠ADC=∠ADB+∠BDC=90°
∴AC是⊙O的直径;
(2)作AM⊥BD于M,CN⊥BD于N
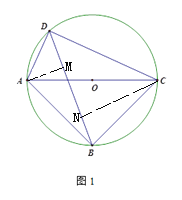
∵∠BDC=∠ADB =45°
∴△ADM,△CDN为等腰直角三角形
∴DM=AM=![]() AD, DN=CN=
AD, DN=CN=![]() CD
CD
∵AC是直径,∠BAC=45°
∴△ABC为等腰直角三角形
∴∠ABC =∠ABM+∠NBC=90°,AB=BC
∵AM⊥BD,CN⊥BD
∴∠AMB=∠BNC=∠BCN+∠NBC =90°
∴∠ABM=∠BCN
△ABM≌△BCN
∴BN=AM=DM=![]() AD
AD
∵AD+CD=5![]()
∴BD=BN+DN=![]() AD+
AD+![]() CD=
CD=![]() ×5
×5![]() =5;
=5;
(3)延长DA到点F,使得AF=CD,连接BF
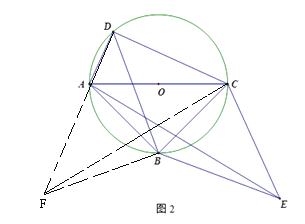
由(2)得BD=![]() (AD+CD)=
(AD+CD)=![]() DF,
DF,
∵∠ADB =45°
∴△BDF为等腰直角三角形
∴BF=BD,DF2=2BD2
连接CF,
在△AFB和△CDB中
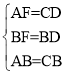
∴△AFB≌△CDB
∴∠ABF=∠CBD
又∵把△DBC沿直线BC翻折得到△EBC
∴∠CBE=∠CBD,BD=BE
∴∠ABF+∠ABC=∠CBE+∠ABC,即∠CBF=∠ABE,BF=BE
∵AB=CB
∴△CBF≌△ABE
∴AE=CF
∴在Rt△FDC中,CF2=DF2+CD2
即AE2=2BD2+CD2.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.

(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=2.
(1)试在图中画出将△ABC以B为旋转中心,沿顺时针方向旋转90°后的图形△A1BC1;
(2)若点B的坐标为(-1,-4),点C的坐标为(-3,-4),试在图中画出直角坐标系,并写出点A的坐标;
(3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该实验,发现摸到绿球的频率稳定于0.25,求n的值;
(2)在该不透明袋子中同时摸出两个球,求摸出的两个球颜色不同的概率.(要求列表或画树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数的图象经过A(1,m),B(2,n),C(4,t),且点B是该二次函数图象的顶点.
(1)若m=3,n=4,求二次函数解析式;
(2)请在图中描出该函数图象上另外的两个点,并画出图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带的BC边长为x m,绿化带的面积为y m2.
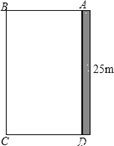
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,满足条件的绿化带的面积最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司共有汽车50辆,市场调查表明,当租金为每辆每日200元时可全部租出,当租金每提高10元,租出去的车就减少2辆.
(1)当租金提高多少元时,公司的每日收益可达到10120元?
(2)公司领导希望日收益达到10200元,你认为能否实现?若能,求出此时的租金,若不能,请说明理由.
(3)汽车日常维护要一定费用,已知外租车辆每日维护费为100元,未租出的车辆维护费为50元,当租金为多少元时,公司的利润恰好为5500元?(利润=收益一维护费).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
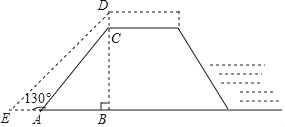
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com