
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() , 点
, 点![]() 与点
与点![]() 关于抛物线的对称轴对称.
关于抛物线的对称轴对称.
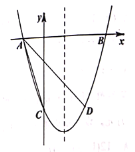
(1)求抛物线的解析式及点![]() 的坐标:
的坐标:
(2)点![]() 是抛物线对称轴上的一动点,当
是抛物线对称轴上的一动点,当![]() 的周长最小时,求出点
的周长最小时,求出点![]() 的坐标;
的坐标;
(3)点![]() 在
在![]() 轴上,且
轴上,且![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
【答案】(1) 解析式为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)
;(3) ![]() 点坐标为
点坐标为![]() 或
或![]()
【解析】
(1)利用待定系数法即可求出n,利用对称性C、D关于对称轴对称即可求出点D坐标.
(2)A,P,D三点在同一直线上时△PAC的周长最小,求出直线AD的解析式即可解决问题.
(3)分两种情形①作DQ∥AC交x轴于点Q,此时∠DQA=∠DAC,满足条件.②设线段AD的垂直平分线交AC于E,直线DE与x的交点为Q′,此时∠Q′DA=′CAD,满足条件,分别求解即可.
解: (1)根据题意得, ![]()
解得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]()
![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]()
![]() 点
点![]() 与点
与点![]() 关于抛物线的对称轴对称
关于抛物线的对称轴对称
![]() 点
点![]() 的坐标为
的坐标为![]()
(2)连接![]()
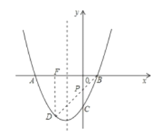
![]() 点
点![]() 与点
与点![]() 关于抛物线的对称轴对称.
关于抛物线的对称轴对称.
![]()
![]()
![]() 为定值,
为定值,![]()
![]() 当的
当的![]() 值最小
值最小
即![]() 三点在同一直线上时
三点在同一直线上时![]() 的周长最小
的周长最小
由![]() 解得,
解得,![]()
![]() 在
在![]() 的左侧,
的左侧,![]()
由![]() 两点坐标可求得直线
两点坐标可求得直线![]() 的解析式为
的解析式为![]()
当![]() 时,
时,![]()
![]() 当
当![]() 的周长最小时,点
的周长最小时,点![]() 的坐标为
的坐标为![]()
(3) ![]() 点坐标为
点坐标为![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带的BC边长为x m,绿化带的面积为y m2.
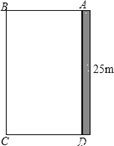
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,满足条件的绿化带的面积最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 的对称轴为
的对称轴为![]() ,且经过点A(2,1),点
,且经过点A(2,1),点![]() 是抛物线上的动点,
是抛物线上的动点,![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,
,![]() ,过点A作AE⊥x轴,垂足为E.则当
,过点A作AE⊥x轴,垂足为E.则当![]() ( )时,
( )时,![]() 的周长最小.
的周长最小.
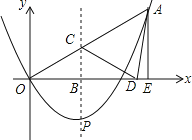
A.1B.1.5C.2D.2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市新建了圆形文化广场,小杰和小浩准备不同的方法测量该广场的半径.
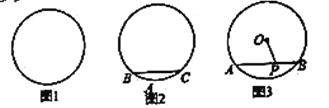
(1)小杰先找圆心,再量半径,请你在图1中,用尺规作图的方法帮小杰找到该广场的圆心![]() (不写作法,保留作图痕迹);
(不写作法,保留作图痕迹);
(2)小浩在广场边(如图2)选取![]() 、
、![]() 、
、![]() 三根石柱,量得
三根石柱,量得![]() 、
、![]() 之间的距离与
之间的距离与![]() 、
、![]() 之间的距离相等,并测得
之间的距离相等,并测得![]() 长为240米,
长为240米,![]() 到
到![]() 的距离为5米.请你帮他求出广场的半径;
的距离为5米.请你帮他求出广场的半径;
(3)请你解决下面的问题:如图3,![]() 的直径为
的直径为![]() ,弦
,弦![]() ,
,![]() 是弦
是弦![]() 上的一个动点,求出
上的一个动点,求出![]() 的长度范围是多少?
的长度范围是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
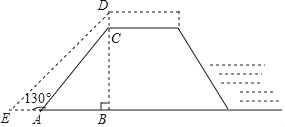
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次聚会上,规定每两个人见面必须握手,且握手1次.
(1)若参加聚会的人数为3,则共握手 次;若参加聚会的人数为5,则共握手 次;
(2)若参加聚会的人数为n(n为正整数),则共握手 次;
(3)若参加聚会的人共握手28次,请求出参加聚会的人数.
(4)嘉嘉由握手问题想到了一个数学问题:若线段AB上共有m个点(不含端点A,B),线段总数为多少呢?请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() .
.
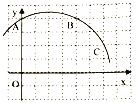
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为________.
(2)点D坐标为![]() ,连接CD,判断直线CD与⊙M的位置关系并说明理由.
,连接CD,判断直线CD与⊙M的位置关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形CEFG的边长分别为a和b,BE和DG相交于点H,连接HC,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确的结论是__________.
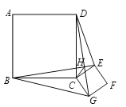
查看答案和解析>>
科目:初中数学 来源: 题型:
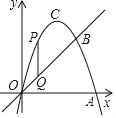
【题目】如图,在平面直角坐标系xOy中,抛物线顶点为C(1,2),且与直线y=x交于点B(![]() ,
,![]() );点P为抛物线上O,B两点之间一个动点(不与O,B两点重合),过P作PQ∥y轴交线段OB于点Q.
);点P为抛物线上O,B两点之间一个动点(不与O,B两点重合),过P作PQ∥y轴交线段OB于点Q.
(1)求抛物线的解析式;
(2)当PQ的长度为最大值时,求点Q的坐标;
(3)点M为抛物线上O,B两点之间一个动点(不与O,B两点重合),点N为线段OB上一个动点;当四边形PQNM为平行四边形,且PN⊥OB时,请直接写出Q点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com