练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，直立于地面上的电线杆，在阳光下落在水平地面和坡面上的影子分别是.测得， ， ，在D处测得电线杆顶端A的仰角为，则电线杆的高度为（ ）

    A. B. C. D.

    【答案】B

    【解析】分析：延长AD交BC的延长线于E，作DF⊥BE于F，在Rt△DFC中，根据直角三角形的性质和勾股定理求出DF、CF的长；在Rt△DFE中，根据正切的定义求出EF，得到BE的长；在Rt△ABE中，根据正切的定义解答即可．

    详解：延长AD交BC的延长线于E，作DF⊥BE于F，

    ∵∠BCD=150°，

    ∴∠DCF=30°，又CD=4，

    ∴DF=2，CF==2 ，

    由题意得∠E=30°，

    ∴EF==2，

    ∴BE=BC+CF+EF=6+4，

    ∴AB=BE×tanE=（6+4）×=（2+4）米，

    即电线杆的高度为（2+4）米．

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（3分）如图，轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行，在B处观测灯塔A位于南偏东50°方向上，轮船航行40分钟到达C处，在C处观测灯塔A位于北偏东10°方向上，则C处与灯塔A的距离是（ ）

    A．20海里 B．40海里 C．海里 D．海里

    查看答案和解析>>

    科目：初中数学 来源： 题型：

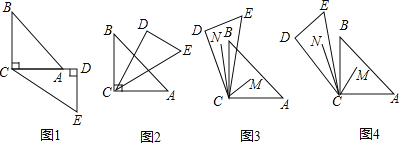
    【题目】将一副三角板如图①摆放，，现将绕点以的速度逆时针旋转，旋转时间为.

    （1）为多少时，恰好平分？请在图②中自己画图，并说明理由；

    （2）当6﹤t﹤8时，平分∠ACE，平分，求，在图中③中完成；

    （3）当8﹤t﹤12时，（2）中的结论是否发生变化？请在图④中完成.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

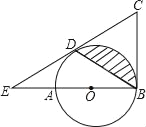
    【题目】如图，AB是⊙O的直径，BC是⊙O的切线，D为⊙O上的一点，CD=CB，延长CD交BA的延长线于点E，

    （1）求证：CD为⊙O的切线；

    （2）若EA=BO=2，求图中阴影部分的面积（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现代互联网技术的广泛应用，催生了快递行业的高速发展，据调查，某家快递公司，今年三月份与五月份完成投递的快件总件数分别是5万件和万件，现假定该公司每月投递的快件总件数的增长率相同．

    求该公司投递快件总件数的月平均增长率；

    如果平均每人每月可投递快递万件，那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，C、D是线段AB上两点，M、N分别是线段AD、BC的中点，下列结论：①若AD=BM，则AB=3BD；②若AC=BD，则AM=BN；③AC-BD=2（MC-DN）；④2MN=AB-CD．其中正确的结论是（ ）

    A.①②③B.③④C.①②④D.①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知∠MON=140°，∠AOC与∠BOC互余，OC平分∠MOB，

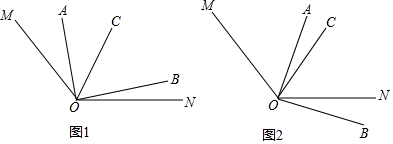
    （1）在图1中，若∠AOC=40°，则∠BOC= °，∠NOB= °．

    （2）在图1中，设∠AOC=α，∠NOB=β，请探究α与β之间的数量关系（ 必须写出推理的主要过程，但每一步后面不必写出理由）；

    （3）在已知条件不变的前提下，当∠AOB绕着点O顺时针转动到如图2的位置，此时α与β之间的数量关系是否还成立？若成立，请说明理由；若不成立，请直接写出此时α与β之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

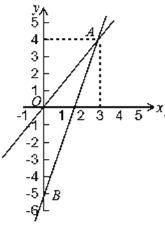
    【题目】如图，一个正比例函数与一个一次函数的图象交于点A（3，4），其中一次函数与y轴交于B点，且OA＝OB．

    （1）求这两个函数的表达式；

    （2）求△AOB的面积S．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面直角坐标系xOy中，直线y＝x+b与直线y＝x交于点A（m，1）．与y轴交于点B

    （1）求m的值和点B的坐标；

    （2）若点C在y轴上，且△ABC的面积是1，请直接写出点C的坐标．

    查看答案和解析>>

    同步练习册答案