
【题目】如图1,在矩形ABCD中,E是AD上的一点,点P从点B沿折线BE﹣ED﹣DC,运动到点C时停止;点Q从点B沿BC运动到点C时停止,速度均为每秒1个单位长度,如果点P,Q同时开始运动,设运动时间为t,△BPQ的面积为y,已知y与t的函数图象如图2所示,以下结论:①BC=10; ②cos∠ABE=![]() ;③当t=12时,△BPQ是等腰三角形;④当14≤t≤20时,y=110﹣5t,其中正确的有( )
;③当t=12时,△BPQ是等腰三角形;④当14≤t≤20时,y=110﹣5t,其中正确的有( )
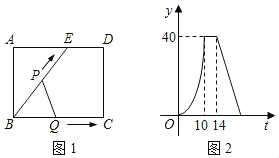
A.1个B.2个C.3个D.4个
【答案】B
【解析】
由图象可知,当10≤t≤14时,y值不变,则此时,Q点到C,P从E到D.
得到BE=BC=10,ED=4故可判断①,根据勾股定理求出AB,再根据cos∠ABE=![]() 求出,即可判断②,求出t=12时,P在点E右侧2单位,利用勾股定理得到PC的长,即可判断③,当14≤t≤20时,点P由D向C运动,Q在C点,根据三角形的面积公式△BPQ的面积为
求出,即可判断②,求出t=12时,P在点E右侧2单位,利用勾股定理得到PC的长,即可判断③,当14≤t≤20时,点P由D向C运动,Q在C点,根据三角形的面积公式△BPQ的面积为![]() ×10×(22﹣t)即可判断④.
×10×(22﹣t)即可判断④.
解:由图象可知,当10≤t≤14时,y值不变,则此时,Q点到C,P从E到D.
∴BE=BC=10,ED=4故①正确.
∴AE=6,
Rt△ABE中,AB=![]() ,
,
∴cos∠ABE=![]() 故②错误;
故②错误;
t=12时,P在点E右侧2单位,此时BP>BE=BC,
PC=![]() ,
,
∴△BPQ不是等腰三角形.故③错误;
当14≤t≤20时,点P由D向C运动,Q在C点,
△BPQ的面积为![]() ×10×(22﹣t)=110﹣5t,则④正确.
×10×(22﹣t)=110﹣5t,则④正确.
∴正确的有①④共2个.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c过等腰Rt△OAB的A,B两点,点B在点A的右侧,直角顶点A(0,3).
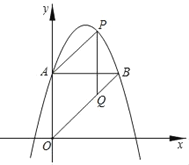
(1)求b,c的值.
(2)P是AB上方抛物线上的一点,作PQ⊥AB交OB于点Q,连接AP,是否存在点P,使四边形APQO是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠A=60°,点O为AB上一点,且3AO=AB,以OA为半径作半圆O,交AC于点D,AB于点E,DE与OC相交于F.
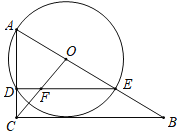
(1)求证:CB与⊙O相切;
(2)若AB=6,求DF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
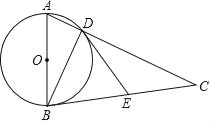
【题目】如图,在锐角△ABC中,以AB为直径的⊙O交AC于点D,过点D作⊙O的切线DE交边BC于点E,连结BD.
(1)求证:∠ABD=∠CDE.
(2)若AC=28,tanA=2,AD:DC=1:3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
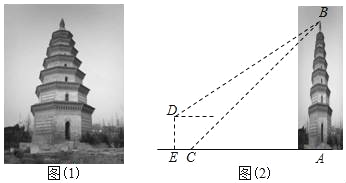
【题目】如图(1),在豫西南邓州市大十字街西南方,耸立着一座古老建筑﹣福胜寺梵塔,建于北宋天圣十年(公元1032年),当地民谚云:“邓州有座塔,离天一丈八.”学完了三角函数知识后,某校“数学社团”的刘明和王华决定用自己学到的知识测量“福胜寺梵塔”的高度.如图(2),刘明在点C处测得塔顶B的仰角为45°,王华在高台上的点D处测得塔顶B的仰角为40°,若高台DE高为5米,点D到点C的水平距离EC为1.3米,且A、C、E三点共线,求该塔AB的高度.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
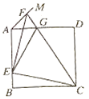
【题目】如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且![]() ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②
,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②![]() 的周长为
的周长为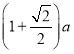 ;③
;③![]() ;④
;④![]() 的面积的最大值
的面积的最大值![]() .其中正确的结论是____.(填写所有正确结论的序号)
.其中正确的结论是____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,点 D 为边 BC 的点,点 E、F 分别是边 AB、AC 上两点,且 EF∥BC,若 AE:EB=m,BD:DC=n,则( )
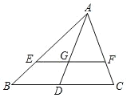
A.若 m>1,n>1,则 2S△AEF>S△ABDB.若 m>1,n<1,则 2S△AEF<S△ABD
C.若 m<1,n<1,则 2S△AEF<S△ABDD.若 m<1,n>1,则 2S△AEF<S△ABD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具用品商店销售A、B两种款式文具盒,已知购进1个A款文具盒比B款文具盒便宜5元,且用300元购入A款文具盒的数量比购入B款文具盒的数量多5个.
(1)购进一个A款文具盒、一个B款文具盒各需多少元?
(2)若A款文具盒与B款文具盒的售价分别是20元和30元,现该文具用品商店计一划用不超过1000元购入共计60个A、B两种款式的文具盒,且全部售完,问如何安排进货才能使销售利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com