
【题目】已知直线![]() .
.
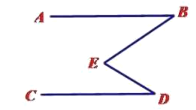
(1)如下图,点![]() 在直线
在直线![]() 的左侧,请写出
的左侧,请写出![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由:
之间的数量关系,并说明理由:
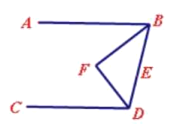
(2)如下图,当点![]() 在线段
在线段![]() 上时,
上时,![]() 分别平分
分别平分![]() ,
,![]() ,此时
,此时![]() 的度数为_________°
的度数为_________°
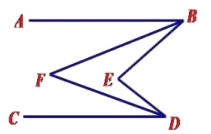
(3)如下图,当点![]() 在直线
在直线![]() 的左侧时,
的左侧时,![]() 分别平分
分别平分![]() ,
,![]() ,请直接写出
,请直接写出![]() 和
和![]() 的数量关系 ;
的数量关系 ;
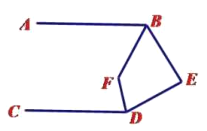
(4)如下图,当点![]() 在直线
在直线![]() 的右侧时,
的右侧时,![]() 分别平分
分别平分![]() ,
,![]() ,请直接写出
,请直接写出![]() 和
和![]() 的数量关系 ;
的数量关系 ;
【答案】(1)∠ABE+∠CDE=∠BED,理由见解析;(2)90;(3)∠BFD=![]() ∠BED;(4)2∠BFD+∠BED=360°
∠BED;(4)2∠BFD+∠BED=360°
【解析】
(1)首先作EF∥AB,根据直线AB∥CD,可得EF∥CD,所以∠ABE=∠1,∠CDE=∠2,据此推得∠ABE+∠CDE=∠BED即可.
(2)作GF∥AB,根据∠ABD+∠CDB=180°,![]() 分别平分
分别平分![]() ,
,![]() ,得到∠BFD=∠BFG+∠DFG=∠ABF+∠CDF=
,得到∠BFD=∠BFG+∠DFG=∠ABF+∠CDF=![]() (∠ABD+∠CDB)=90°;
(∠ABD+∠CDB)=90°;
(3)首先根据BF,DF分别平分∠ABE,∠CDE,推得∠ABF+∠CDF=![]() (∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CDF,∠BED=∠ABE+∠CDE,据此推得∠BFD=
(∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CDF,∠BED=∠ABE+∠CDE,据此推得∠BFD=![]() ∠BED.
∠BED.
(4)首先过点E作EG∥CD,再根据AB∥CD,EG∥CD,推得AB∥CD∥EG,所以∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,据此推得∠ABE+∠CDE+∠BED=360°;然后根据∠BFD=∠ABF+∠CDF,以及BF,DF分别平分∠ABE,∠CDE,推得2∠BFD+∠BED=360°即可.
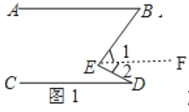
(1)∠ABE+∠CDE=∠BED.
理由:如图1,作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠ABE=∠1,∠CDE=∠2,
∴∠ABE+∠CDE=∠1+∠2=∠BED,
即∠ABE+∠CDE=∠BED.
故答案为:∠ABE+∠CDE=∠BED;
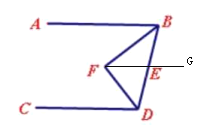
(2)如图,作GF∥AB,
∴AB∥GF∥CD
∴∠ABD+∠CDB=180°,∠BFG=∠ABF,∠DFG=∠CDF
∵![]() 分别平分
分别平分![]() ,
,![]() ,
,
∴∠BFD=∠BFG+∠DFG=∠ABF+∠CDF=![]() ∠ABD +
∠ABD +![]() ∠CDB =
∠CDB =![]() (∠ABD+∠CDB)=90°,
(∠ABD+∠CDB)=90°,
故答案为:90;
(3)∠BFD=![]() ∠BED.
∠BED.
理由:如图
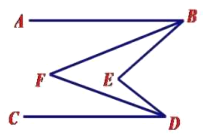
∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
由(1)可得∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE)
(∠ABE+∠CDE)
又∠BED=∠ABE+∠CDE,
∴∠BFD=![]() ∠BED.
∠BED.
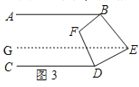
(4)2∠BFD+∠BED=360°.
理由:如图3,过点E作EG∥CD,
∵AB∥CD,EG∥CD,
∴AB∥CD∥EG,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠CDE+∠BED=360°,
由(1)知,∠BFD=∠ABF+∠CDF,
又∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠BFD=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
∴2∠BFD+∠BED=360°.
故答案为:2∠BFD+∠BED=360°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )

A.2:5 B.14:25 C.16:25 D.4:21
查看答案和解析>>
科目:初中数学 来源: 题型:
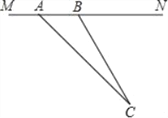
【题目】“为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.
(1)求观测点C到公路MN的距离;
(2)请你判断该汽车是否超速?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(2t,0),B(0,-2t),C(2t,4t)三点,其中t>0,函数![]() 的图象分别与线段BC,AC交于点P,Q.若S△PAB-S△PQB=t,则t的值为__.
的图象分别与线段BC,AC交于点P,Q.若S△PAB-S△PQB=t,则t的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com