
【题目】如图,E,F是平行四边形ABCD对角线BD上的两点,DE=EF=BF,连接CE并延长交AD于点G,连接CF并延长交AB于点H,连接CH,设△CDG的面积为S1,△CHG的面积为S2,则S1与S2的关系正确的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
首先根据平行四边形的性质和题干中的数量关系,可证明点G,H分别是AD,AB的中点;进而得到S1=S△CDG=S△BCH=![]() SABCD;再根据△AGH与△ADB的相似关系,可证得S△AGH=
SABCD;再根据△AGH与△ADB的相似关系,可证得S△AGH=![]() S△ABC=
S△ABC=![]() SABCD,通过SABCD、S△AGH、S△CDG、S△BCH的数量关系,可将S2表示为S2=
SABCD,通过SABCD、S△AGH、S△CDG、S△BCH的数量关系,可将S2表示为S2=![]() SABCD,对比S1
SABCD,对比S1![]() SABCD,最终可得S1与S2的关系.
SABCD,最终可得S1与S2的关系.
∵DE=EF=BF,
∴DF=2BF,BE=2DE
∵四边形ABCD是平行四边形
∴AD∥BC,AB∥CD,AB=CD,AD=BC
∴![]() ,
,![]()
∴CD=2HB,BC=2DG
∴点G,H分别是AD,AB的中点,
∴S1=S△CDG=S△BCH=![]() SABCD,GH∥DB
SABCD,GH∥DB
∵GH∥DB
∴△AGH∽△ADB
∴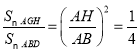
∴S△AGH=![]() S△ABC=
S△ABC=![]() SABCD,
SABCD,
∵S△CHG=SABCD-S△AGH-S△CDG-S△BCH,
∴S2=S△CHG=![]() SABCD,
SABCD,
∴S1=![]() S2,
S2,
故选:C.


科目:初中数学 来源: 题型:
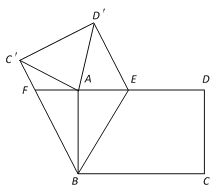
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AD边上的一个动点,将四边形BCDE沿直线BE折叠,得到四边形BC′D′E,连接AC′,AD′.
(1)若直线DA交BC′于点F,求证:EF=BF;
(2)当AE=![]() 时,求证:△AC′D′是等腰三角形;
时,求证:△AC′D′是等腰三角形;
(3)在点E的运动过程中,求△AC′D′面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
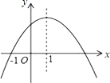
【题目】如图是二次函数![]() 的图象过点(-1,0),其对称轴为
的图象过点(-1,0),其对称轴为![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④此二次函数的最大值是
;④此二次函数的最大值是![]() ,其中结论正确的是( )
,其中结论正确的是( )
A. ①②B. ②③C. ②④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
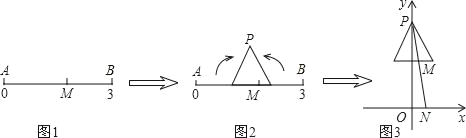
【题目】李老师从“淋浴龙头”受到启发,编了一个题目:在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1;将AB折成正三角形,使点A,B重合于点P,如图2;建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),PM与x轴交于点N(n,0),如图3.当m=![]() 时,n=_____.
时,n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点
的图象交于点![]() 、点
、点![]() .
.
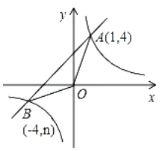
(1)求一次函数和反比例函数的解析式;
(2)求![]() 的面积;
的面积;
(3)直接写出一次函数值大于反比例函数值的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北盘江大桥坐落于云南宜威与贵州水城交界处,横跨云贵两省,为目前世界第一高桥图1是大桥的实物图,图2是从图1中引申出的平面图,测得桥护栏BG=1.8米,拉索AB与护栏的夹角是26°,拉索ED与护栏的夹角是60°,两拉索底端距离BD为300m,若两拉索顶端的距离AE为90m,请求出立柱AH的长.(tan26°≈0.5,sin26°≈0.4,![]() 1.7)
1.7)
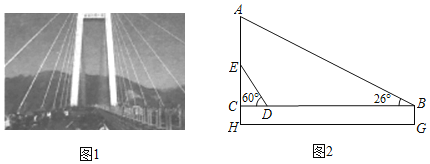
查看答案和解析>>
科目:初中数学 来源: 题型:
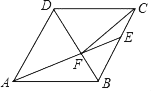
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC,BD于点E,F,CE=2,连接CF.给出以下结论:①△ABF≌△CBF;②点E到AB的距离是3![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中正确的结论序号是_____
.其中正确的结论序号是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
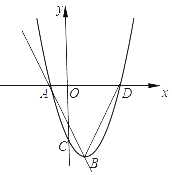
【题目】如图,已知抛物线y=x2+ax﹣3交x轴于点A,D两点,交y轴于点C,过点A的直线与x轴下方的抛物线交于点B,已知点A的坐标是(﹣1,0).
(1)求a的值;
(2)连结BD,求△ADB面积的最大值;
(3)当△ADB面积最大时,求点C到直线AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示.下列说法错误的是
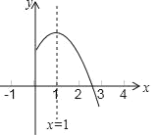
A. abc<0B. a﹣b+c<0C. 3a+c<0D. 当﹣1<x<3时,y>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com