
【题目】在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
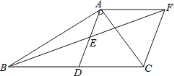
![]() 求证:
求证:![]() ;
;
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是菱形,并证明.
是菱形,并证明.
【答案】![]() 证明见解析;
证明见解析; ![]() 是直角三角形时,四边形
是直角三角形时,四边形![]() 是菱形,理由见解析.
是菱形,理由见解析.
【解析】
(1)根据线段中点的定义可得AE=DE,根据“两直线平行,内错角相等”可得∠EAF=∠EDB,然后利用“角边角”证明△AEF和△DEB全等;
(2)根据全等三角形对应边相等可得AF=BD,根据直角三角形斜边上的中线等于斜边的一半求出AD=BD=CD,再根据一组对边平行且相等的四边形是平行四边形求出四边形ADCF是平行四边形,然后根据邻边相等的平行四边形是菱形证明即可.
![]() 证明:∵
证明:∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,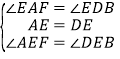 ,
,
∴![]() ;
;
![]() 解:
解:![]() 是直角三角形时,四边形
是直角三角形时,四边形![]() 是菱形.
是菱形.
理由如下:∵![]() ,
,
∴![]() ,
,
∵![]() 是直角三角形,
是直角三角形,![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四形![]() 是平行四边形,
是平行四边形,
又∵![]() ,
,
∴四边形![]() 是菱形.
是菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某地地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款![]() 元,第三天收到捐款
元,第三天收到捐款![]() 元.
元.
![]() 如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
![]() 按照
按照![]() 中收到捐款的增长率不变,该单位三天一共能收到多少捐款?
中收到捐款的增长率不变,该单位三天一共能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,l1和l2分别是走私船和我公安快艇航行路程与时间的函数图象,请结合图象解决下列问题:
(1)在刚出发时,我公安快艇距走私船多少海里?
(2)计算走私船与公安艇的速度分别是多少?
(3)求出l1,l2的解析式.
(4)问6分钟时,走私船与我公安快艇相距多少海里?

查看答案和解析>>
科目:初中数学 来源: 题型:
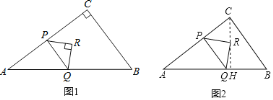
【题目】如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿线段
个单位长度的速度沿线段![]() 运动,到点
运动,到点![]() 停止.当点
停止.当点![]() 不与
不与![]() 的顶点重合时,过点
的顶点重合时,过点![]() 作其所在直角边的垂线交
作其所在直角边的垂线交![]() 于点
于点![]() ,再以
,再以![]() 为斜边作等腰直角三角形
为斜边作等腰直角三角形![]() ,且点
,且点![]() 与
与![]() 的另一条直角边
的另一条直角边![]() 始终在
始终在![]() 同侧,设
同侧,设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() (平方单位),点
(平方单位),点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
![]() 求
求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
![]() 当
当![]() 为何值时点
为何值时点![]() 恰好落在
恰好落在![]() 上?
上?
![]() 当点
当点![]() 在
在![]() 边上运动时,求
边上运动时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 如图
如图![]() ,当
,当![]() 为何值时,点
为何值时,点![]() 恰好落在
恰好落在![]() 边上的高
边上的高![]() 上?
上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=6,求图中阴影部分的面积(结果保留根号和π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,图2,图3,在![]() 中,分别以
中,分别以![]() ,
,![]() 为边,向
为边,向![]() 外作正三角形,正四边形,正五边形,
外作正三角形,正四边形,正五边形,![]() ,
,![]() 相交于点O.
相交于点O.
①如图1,求证:![]() ≌
≌![]() ;
;
②探究:如图1,![]() ________;如图2,
________;如图2,![]() _______;如图3,
_______;如图3,![]() _______;
_______;
(2)如图4,已知:![]() ,
,![]() 是以
是以![]() 为边向
为边向![]() 外所作正n边形的一组邻边:
外所作正n边形的一组邻边:![]() ,
,![]() 是以
是以![]() 为边向
为边向![]() 外所作正n边形的一组邻边,
外所作正n边形的一组邻边,![]() ,
,![]() 的延长相交于点O.
的延长相交于点O.
①猜想:如图4,![]() (用含n的式子表示);
(用含n的式子表示);
②根据图4证明你的猜想.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com