练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    四边形ABCD中，对角线AC、BD相交于点O，给出下列四组条件：①AB∥CD，AD∥BC；②AB=CD，AD=BC；③AO=CO，BO=DO；④AB∥CD，AD=BC．其中一定能判定这个四边形是平行四边形的条件有    

        A．1组          B．2组         C．3组          D．4组


    C


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    在“老年节” 前夕，某公司工会组织323名退休职工到浙江杭州旅游，旅游前，工会确定每车保证有一名随团医生，并为此次旅游请了8名医生，现打算同时租甲、乙两种客车，其中甲种客车每辆载客50人，乙种客车每辆载客20人。

    （1）请帮助工会设计租车方案。

    （2）若甲种客车租金为800元/辆，乙种客车租金为600元/辆，工会按哪种方案租车最省钱？此时租金是多少？

    （3）旅游前，一名医生由于有特殊情况，工会只能安排7名医生随团，为保证所租的每辆车安排有一名医生，租车方案调整为：同时租80座、50座和20座的大小三种客车，出发时，所租的三种客车的座位恰好坐满，请问工会的租车方案如何安排？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知二次函数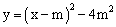（m＞0）的图象与x轴交于A、B两点．

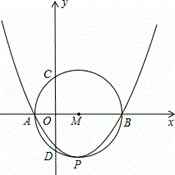
    （1）写出A、B两点的坐标（坐标用m表示）；

    （2）若二次函数图象的顶点P在以AB为直径的圆上，求二次函数的解析式；

    （3）设以AB为直径的⊙M与y轴交于C、D两点，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图是9×7的正方形点阵，其水平方向和竖起直方向的两格点间的长度都为1个单位，以这些点为顶点的三角形称为格点三角形．请通过画图分析、探究回答下列问题：

    (1)请在图中画出以AB为边且面积为2的一个网格三角形；

    (2)任取该网格中能与A、B构成三角形的一点M，求以A、B、M为顶点的三角形的面积为2的概率；

    (3)任取该网格中能与A、B构成三角形的一点M，求以A、B、M为顶点的三角形为直角三角形的概率.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在正方形ABCD中，点E在BC边所在直线上，过E作EF⊥AC于F，G为线段AE的中点，连接BF、FG、GB。

    证明：△BGF是等腰直角三角形。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


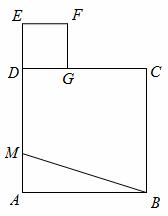
    如图，在边长为3的正方形ABCD中，点M在边AD上，且AM=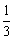AD，延长MD至点E，使ME=MB，以DE为边作正方形DEFG，点G在边CD上，则DG 的长为       。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，⊙O1，⊙O2、相交于A、B两点，两圆半径分别为6cm和8cm，弦AB的长为9.6cm，则两圆的连心线O1O2的长为【    】

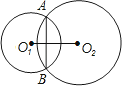
    A．11cm       B．10cm       C．9cm       D．8cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，已知∠BAC=45°，AD⊥BC于D，BD=2，DC=3，求AD的长。

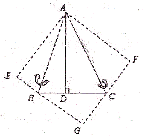
    小萍同学灵活运用了轴对称知识，将图形进行翻折变换，巧妙地解答了此题。

    （1）分别以AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D、C点的对称点分别为E、F，延长EB、FC相交于G点，求证：四边形AEGF是正方形；

    （2）设AD=x，利用勾股定理，建立关于x的方程模型，求出x的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


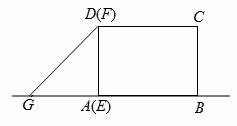
     如图，点G、E、A、B在一条直线上，等腰直角△EFG从如图所示是位置出发，沿直线AB以1单位/秒向右匀速运动，当点G与B重合时停止运动。已知AD=1，AB=2，设△EFG与矩形ABCD重合部分的面积为S平方单位，运动时间为t秒，则S与t的函数关系是         。

    查看答案和解析>>

    同步练习册答案