
【题目】如图,△ABC中,AC=BC,CE为△ABC的中线,BD为AC边上的高,BF平分∠CBD交CE于点G,连接AG交BD于点M,若∠AFG=53°,则∠GAB的度数为__________.

【答案】45°
【解析】
根据等腰三角形三线合一性质得出∠CAB=∠CBA,∠GAB=∠GBA,再根据已知条件依次求出∠ACB=16°,∠CAB=∠CBA=82°,∠GAB=∠GBA=45°即可.
∵AC=BC, CE为△ABC的中线,
∴CE⊥AB,AG =BG,
∴∠CAB=∠CBA,∠GAB=∠GBA,
∵BD为AC边上的高,∠AFG=53°,
∴∠FBD=37°,
∵BF平分∠CBD,
∴∠CBF=∠FBD
∴∠ACB=∠AFG -∠CBF =∠AFG -∠FBD = 53°- 37°=16°,
∴∠CAB=∠CBA= ![]() (180°-∠ACB) =
(180°-∠ACB) =![]() (180°-16°)=82°,
(180°-16°)=82°,
∴∠GAB =∠GBA=∠CAB -∠CBF =82°- 37°= 45°.
故填:45°.


科目:初中数学 来源: 题型:
【题目】如图,一段抛物线y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x 轴于点A2;将C2绕点A2旋转180°得C3 , 交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为 . 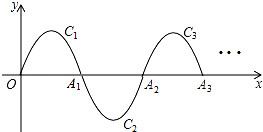
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,从口袋中随机摸出一个小球,记下标号后放回,再从口袋中随机摸出一个小球,记下标号.用画树状图(或列表)的方法,求两次摸出的小球号码恰好都大于1的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则称点
,则称点![]() 是点
是点![]() 的“
的“![]() 演化点”.例如,点
演化点”.例如,点![]() 的“
的“![]() 演化点”为
演化点”为![]() ,即
,即![]() .
.
(1)已知点![]() 的“
的“![]() 演化点”是
演化点”是![]() ,则
,则![]() 的坐标为________;
的坐标为________;
(2)已知点![]() ,且点
,且点![]() 的“
的“![]() 演化点”是
演化点”是![]() ,则
,则![]() 的面积
的面积![]() 为__________;
为__________;
(3)己知![]() ,
,![]() ,
,![]() ,
,![]() ,且点
,且点![]() 的“
的“![]() 演化点”为
演化点”为![]() ,当
,当![]() 时,
时,![]() ___________.
___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD的纸片中,AC⊥AB,AC与BD交于O,将△ABC沿对角线AC翻折得到![]() .
.
(1)求证:四边形ACDB’是矩形.
(2)若平行四边形ABCD的面积为12,求翻折后纸片重叠部分的面积,即![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 . 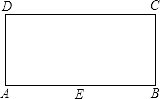
查看答案和解析>>
科目:初中数学 来源: 题型:
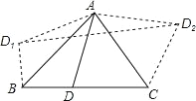
【题目】如图,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2![]() +2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
+2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】白色污染( Whitepollution)是人们对难降解的塑料垃圾(多指塑料袋)污染环境现象的一种形象称谓.为了让全校同学感受丢弃塑料袋对环境的影响,小彬随机抽取某小区![]() 户居民,记录了这些家庭
户居民,记录了这些家庭![]() 年某个月丢弃塑料袋的数量(单位:个)
年某个月丢弃塑料袋的数量(单位:个)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请根据上述数据,解答以下问题:

(1)小彬按“组距为![]() ”列出了如下的频数分布表(每组数据含最小值不含最大值),请将表中空缺的部分补充完整,并补全频数直方图;
”列出了如下的频数分布表(每组数据含最小值不含最大值),请将表中空缺的部分补充完整,并补全频数直方图;
分组 | 划记 | 频数 |
| _______ | ________ |
|
|
|
| _______ | ________ |
|
|
|
合计 | / |
|
(2)根据(1)中的直方图可以看出,这![]() 户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
(3)根据频数分布表,小彬又画出了如图所示的扇形统计图.请将统计图中各组占总数的百分比填在图中,并求出![]() 组对应的扇形圆心角的度数;
组对应的扇形圆心角的度数;
(4)若该小区共有![]() 户居民家庭,请你估计每月丢弃的塑料袋数量不小于
户居民家庭,请你估计每月丢弃的塑料袋数量不小于![]() 个的家庭个数.
个的家庭个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A. (2,5)B. (5,2)C. (2,﹣5)D. (5,﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com