
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则称点
,则称点![]() 是点
是点![]() 的“
的“![]() 演化点”.例如,点
演化点”.例如,点![]() 的“
的“![]() 演化点”为
演化点”为![]() ,即
,即![]() .
.
(1)已知点![]() 的“
的“![]() 演化点”是
演化点”是![]() ,则
,则![]() 的坐标为________;
的坐标为________;
(2)已知点![]() ,且点
,且点![]() 的“
的“![]() 演化点”是
演化点”是![]() ,则
,则![]() 的面积
的面积![]() 为__________;
为__________;
(3)己知![]() ,
,![]() ,
,![]() ,
,![]() ,且点
,且点![]() 的“
的“![]() 演化点”为
演化点”为![]() ,当
,当![]() 时,
时,![]() ___________.
___________.
【答案】(2,14) 20 ![]()
【解析】
(1)根据题意a=3,x=-1,y=5时,求点![]() 的坐标;
的坐标;
(2)根据题意列方程组求点Q的坐标,然后结合坐标系中点的位置,利用割补法求三角形面积;
(3)根据题意求出![]() ,然后分点
,然后分点![]() 在y轴正半轴和负半轴两种情况讨论,利用三角形面积列方程求解.
在y轴正半轴和负半轴两种情况讨论,利用三角形面积列方程求解.
解:(1)由题意可知:点![]() 的“
的“![]() 演化点”是
演化点”是![]() ,即
,即![]() ,
,
故答案为:(2,14)
(2)设Q点坐标为(x,y),由题意可知:![]() ,解得:
,解得:![]()
∴Q点坐标为(0,4)
∴![]()
故答案为:20;
(3)由题意可知:AD=3,OC=5
![]() 的坐标为
的坐标为![]() ,即点
,即点![]() 的坐标为
的坐标为![]()
当点![]() 位于y轴正半轴时,
位于y轴正半轴时,![]() ,
,
∴![]() 或
或![]() (此情况不合题意,舍去)
(此情况不合题意,舍去)
又∵![]()
∴![]() ,解得:
,解得:![]() (舍去)
(舍去)
当点![]() 位于y轴正半轴时,
位于y轴正半轴时,![]() ,
,
∴![]()
又∵![]()
∴![]() ,解得:
,解得:![]() ,即
,即![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】为了适应广大市民锻炼,休闲的需要,某市新修建了一条绿道![]() (如图),父子两人同时从起点
(如图),父子两人同时从起点![]() 出发,沿绿道进行跑步锻炼,到达
出发,沿绿道进行跑步锻炼,到达![]() 点后立即返回向起点
点后立即返回向起点![]() 跑去,他们不断往返于
跑去,他们不断往返于![]() 之间,已知父子两人的速度分别为2米/秒和3米/秒,儿子第一次到达
之间,已知父子两人的速度分别为2米/秒和3米/秒,儿子第一次到达![]() 点时,父亲离
点时,父亲离![]() 点还有1200米,则(1)父亲第一次到达
点还有1200米,则(1)父亲第一次到达![]() 点时,儿子离
点时,儿子离![]() 点的距离是_________米;(2)从起点
点的距离是_________米;(2)从起点![]() 出发后________小时父子两人恰好第一次同时回到起点
出发后________小时父子两人恰好第一次同时回到起点![]() .
.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过A(﹣3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.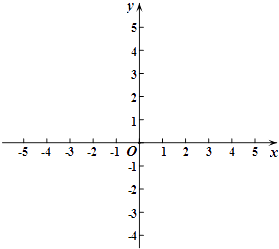
(1)求该抛物线的解析式;
(2)若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;
(3)该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名学生练习计算机打字,甲打一篇1000字的文章与乙打一篇800字的文章所用的时间相同.已知甲每分钟比乙每分钟多打10个字.求甲、乙两人每分钟各打多少字?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅会影响人们的出行,还影响着人们的健康,但是人们到底对雾霾了解多少呢?带着这种思考,某学校九年级综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了本市部分市民的观点(分四类:A类工业污染;B类汽车尾气排放;C类燃煤问题;D类其他原因.调查的每名市民只选择一种类别),并对调查结果进行录入整理,绘制了如下两幅不完整的统计图.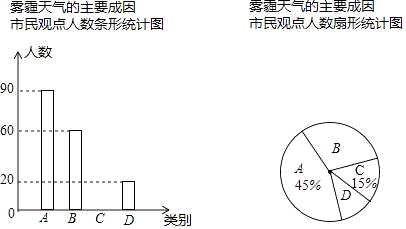
请根据图中提供的信息解答下列问题:
(1)求出本次调查的市民人数,并补全条形统计图.
(2)估计该市800万名市民中持有A、B两类看法的总人数.
(3)结合本次调查结果,请你给出一条“为减少雾霾天气发生”的合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成证明并写出推理根据:如图,直线![]() 分别与直线
分别与直线![]() 、
、![]() 交于点
交于点![]() 和点
和点![]() ,
,![]() ,射线
,射线![]() 、
、![]() 分别与直线
分别与直线![]() 交于点
交于点![]() 、
、![]() ,且
,且![]() ,则
,则![]() 与
与![]() 有何数量关系?并说明理由.
有何数量关系?并说明理由.

解:![]() 与
与![]() 的数量关系为 ① ,理由如下:
的数量关系为 ① ,理由如下:
∵![]() (已知)
(已知)
∴ ② // ② ( ② )
∴![]() ③ ( ③ )
③ ( ③ )
∵![]() (已知)
(已知)
∴ ④ ( ④ )
∵![]() ⑤
⑤
∴![]() ⑥ -
⑥ -![]() ⑥
⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,CE为△ABC的中线,BD为AC边上的高,BF平分∠CBD交CE于点G,连接AG交BD于点M,若∠AFG=53°,则∠GAB的度数为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com