
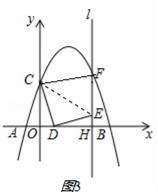
��ͼ1����ƽ��ֱ������ϵ�У�������y=ax2+bx+3��x����A����1��0����B��5��0�����㣬��y���ڵ�C����D���߶�OB��һ���㣬����CD�����߶�CD�Ƶ�D˳ʱ����ת90��õ��߶�DE������E��ֱ��l��x����H������C��CF��l��F��
��1���������߽���ʽ��
��2����ͼ2������Fǡ������������ʱ�����߶�OD�ij���
��3���ڣ�2���������£�
������DF����tan��FDE��ֵ��
����̽����ֱ��l�ϣ��Ƿ���ڵ�G��ʹ��EDG=45�㣿�����ڣ���ֱ��д����G�����ꣻ�������ڣ���˵�����ɣ�


�����㡿���κ����ۺ��⣮
��ר�⡿ѹ���⣮
����������1�����ô���ϵ������ü��ɣ�
��2������C�����������F�����꣬Ȼ��ͨ����OCD�ա�HDE���ó�DH=OC=3���������OD�ij���
��3������ȷ��C��D��E��F�ĵ㹲Բ������Բ�ܽǶ�����á�ECF=��EDF������tan��ECF=
 =
=
 =
=
 ���������tan��FDE=
���������tan��FDE=
 ��
��
������CE���ó���CDE�ǵ���ֱ�������Σ��ó���CED=45�㣬��D����DG1��CE����ֱ��l��G1����D����DG2��CE����ֱ��l��G2�����EDG1=45�㣬��EDG2=45�㣬���ֱ��CE�Ľ���ʽΪy=��
 x+3���������ֱ��DG1�Ľ���ʽΪy=��
x+3���������ֱ��DG1�Ľ���ʽΪy=��
 x+m��ֱ��DG2�Ľ���ʽΪy=2x+n����D��������뼴�����m��n���Ӷ���ý���ʽ���������G�����꣮
x+m��ֱ��DG2�Ľ���ʽΪy=2x+n����D��������뼴�����m��n���Ӷ���ý���ʽ���������G�����꣮
����𡿽⣺��1����ͼ1����������y=ax2+bx+3��x����A����1��0����B��5��0�����㣬
��
 ��
��
���
 ��
��
�������߽���ʽΪy=��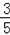
 x2+
x2+
 x+3��
x+3��
��2����ͼ2���ߵ�Fǡ�����������ϣ�C��0��3����


��F��������Ϊ3��
��y=3����y=��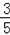
 x2+
x2+
 x+3�ã�3=��
x+3�ã�3=��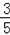
 x2+
x2+
 x+3��
x+3��
���x=0��x=4��
��F��4��3��
��OH=4��
�ߡ�CDE=90�㣬
���ODC+��EDH=90�㣬
���OCD=��EDH��
�ڡ�OCD�͡�HDE�У�

 ��
��
���OCD�ա�HDE��AAS����
��DH=OC=3��
��OD=4��3=1��
��3������ͼ3������CE��

��OCD�ա�HDE��
��HE=OD=1��
��BF=OC=3��
��EF=3��1=2��
�ߡ�CDE=��CFE=90�㣬
��C��D��E��F�ĵ㹲Բ��
���ECF=��EDF��
��RT��CEF����CF=OH=4��
��tan��ECF=
 =
=
 =
=
 ��
��
��tan��FDE=
 ��
��
����ͼ4����CE��


��CD=DE����CDE=90�㣬
���CED=45�㣬
��D����DG1��CE����ֱ��l��G1����D����DG2��CE����ֱ��l��G2�����EDG1=45�㣬��EDG2=45��
��EH=1��OH=4��
��E��4��1����
��C��0��3����
��ֱ��CE�Ľ���ʽΪy=��
 x+3��
x+3��
��ֱ��DG1�Ľ���ʽΪy=��
 x+m��
x+m��
��D��1��0����
��0=��
 ��1+m�����m=
��1+m�����m=
 ��
��
��ֱ��DG1�Ľ���ʽΪy=��
 x+
x+
 ��
��
��x=4ʱ��y=��
 +
+
 =��
=��
 ��
��
��G1��4����
 ����
����
��ֱ��DG2�Ľ���ʽΪy=2x+n��
��D��1��0����
��0=2��1+n�����n=��2��
��ֱ��DG2�Ľ���ʽΪy=2x��2��
��x=4ʱ��y=2��4��2=6��
��G2��4��6����
���ϣ���ֱ��l�ϣ��Ƿ���ڵ�G��ʹ��EDG=45�㣬��G������Ϊ��4����
 ����4��6����
����4��6����


�������������Ƕ��κ������ۺ��⣬�����˴���ϵ��������κ����Ľ���ʽ��һ�κ����Ľ���ʽ��������ȫ�ȵ��ж������ʣ�����ֱ�������ε����ʣ�ƽ���ߵ����ʵȣ����ν��˼���Ӧ���ǽ���Ĺؼ���
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ͼ��ʾ������ABC�Ƶ�A����ʱ����ת30��õ���ADC�䣬���ABD�Ķ����ǣ�������


A��30�� B��45�� C��60�� D��75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ABC���ABD�У�AD��BC�ཻ��O�㣬��1=��2����������һ���������������������߶Σ����ٱ�ע��ʹ��������ĸ����ʹAC=BD��������֤����
�����ӵ������ǣ��� ����
֤������ ����
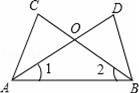

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ijЬ����A��B��C��D�Ŀ��˶�Ь��Ԫ���ڼ�㡰��һ��һ�������������״ͼ����������ѡȡ���ͬ���˶�Ь��ǡ��ѡ��A��C����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���������ж�AB��CD�������У�����������
��1����B+��BCD=180�㣻��2����1=��2����3����3=��4����4����B=��5��


A��1 B��2 C��3 D��4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com