

分析 (1)根据零指数幂与负整数指数幂的意义计算;
(2)利用代入消元法解方程组;
(3)①连结AA1、BB1即可得到对称中心E点,如图1,然后写出点E、A、C1的坐标;
②由于P(a,b)平移后点P的对应点为P2(a+6,b+2),则可判断△ABC向右平移6个单位,再向上平移2个单位得到△A2B2C2,则根据点规律得到点A2、B2、C2的坐标,然后描点即可;
(4)①从条形统计图中得到五个数据,然后根据众数和平均数的定义求解;
②先用一天闯红灯的总人次乘以未成年人所占的百分比得到这天未成年人闯红灯的人次数,然后乘以30即可;
③可针对闯红灯的高峰时间段加强管理或对不同人群加强教育等.
解答 (1)解:原式=1-2+3$\sqrt{3}$-5-2$\sqrt{3}$=$\sqrt{3}$-6;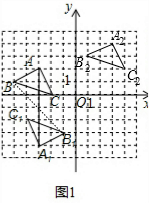
(2)解:$\left\{\begin{array}{l}{5x+y=2①}\\{x-3y-4=0②}\end{array}\right.$,
由①得y=2-5x③,
把③代入②得x-3(2-5x)-4=0,
解得x=$\frac{5}{8}$,
把x=$\frac{5}{8}$代入③得x=2-5×$\frac{5}{8}$=-$\frac{9}{8}$,
所以方程组的解为$\left\{\begin{array}{l}{x=\frac{5}{8}}\\{y=-\frac{9}{8}}\end{array}\right.$;
(3)解:①连结AA1、BB1,则交点为对称中心E点,如图1,其中E(-3,-1)、A(-3,2)、C1(-4,-2);
②如图1,A2(3,4)、C2(4,2);
(4)解:①因为图中的五个数据为20、15、10、15、40,
所以这组数据的众数为15、平均数为20;
②100×(1-15%-55%)×30=900(人),
估计一个月(按30天计算)上午7:00~12:00在该十字路口闯红灯的未成年人约有900人次;
③加强对11~12点时段的交通管理.
故答案为900.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了实数的运算、解二元一次方程组和统计图.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一座拱桥的轮廓是抛物线型,拱高OC为6m,跨度AB为20m.
如图,一座拱桥的轮廓是抛物线型,拱高OC为6m,跨度AB为20m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
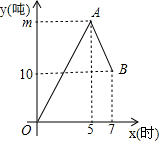 某仓库有甲、乙、丙三辆运货车,在满载的情况下,甲车每小时可运货6吨,乙车每小时可运货10吨,某天只有乙车负责进货,甲车和丙车负责出货.如图是从早晨上班开始库存量y(吨)与时间x(时)之间的函数图象,OA段表示甲、乙两车一起工作,AB段表示乙、丙两车一起工作,且在工作期间,每辆车都是满载的.
某仓库有甲、乙、丙三辆运货车,在满载的情况下,甲车每小时可运货6吨,乙车每小时可运货10吨,某天只有乙车负责进货,甲车和丙车负责出货.如图是从早晨上班开始库存量y(吨)与时间x(时)之间的函数图象,OA段表示甲、乙两车一起工作,AB段表示乙、丙两车一起工作,且在工作期间,每辆车都是满载的.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com