
【题目】为了解全校学生上学的交通方式,该校九年级(8)班的4名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式) 设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息, 解答下列问题:
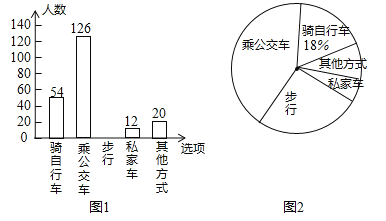
(1)本次接受调查的总人数是 人, 并把条形统计图补充完整;
(2)在扇形统计图中,“步行”的人数所占的百分比是 ,“其他方式”所在扇形的圆心角度数是 ;
(3)已知这4名同学中有2名女同学,要从中选两名同学汇报调查结果.请你用列表法或画树状图的方法, 求出恰好选出1名男生和1名女生的概率.
【答案】(1)图见解析;300(2)29.3%;24(3)![]()
【解析】
(1)根据上学方式为“骑自行车”的学生数除以所占的百分比即可求出调查的学生总数;根据总学生数求出上学方式为“步行”的学生数,补全条形统计图即可;
(2)由![]() ×100%可以求得在扇形统计图中 “步行”的人数所占的百分比;同理求得“其他方式”所占的百分比,进而求得“其他方式”所在扇形的圆心角度数;
×100%可以求得在扇形统计图中 “步行”的人数所占的百分比;同理求得“其他方式”所占的百分比,进而求得“其他方式”所在扇形的圆心角度数;
(3)根据题意画出树状图,得出所有等情况数和恰好选出1名男生和1名女生的情况,再根据概率公式计算即可.
(1)本次接受调查的总人数是:54÷18%=300(人),
步行的人数有:300541261220=88(人),补图如下:
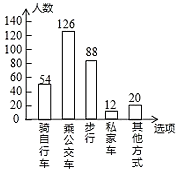
故答案为:300;
(2)在扇形统计图中,“步行”的人数所占的百分比是:![]() ×100%=29.3%;
×100%=29.3%;
“其他方式”所在扇形的圆心角度数是:360![]() ×
×![]() ×100%=24
×100%=24![]() .
.
故答案是:29.3%;24;
(3)根据题意列表如下:
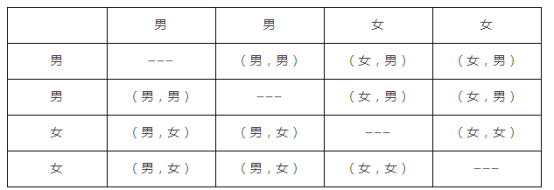
得到所有等可能的情况有12种,其中恰好抽中一男一女的情况有8种,
则P(一男一女)=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】“农民也能报销医疗费了!”这是国家推行新型农村医疗合作的成果.村民只要每人每年交10元钱,就可以加入合作医疗,每年先由自己支付医疗费,年终时可得到按一定比例返回的返回款,这一举措极大地增强了农民抵御大病风险的能力.小华与同学随机调查了他们乡的一些农民,根据收集到的数据绘制了以下的统计图.
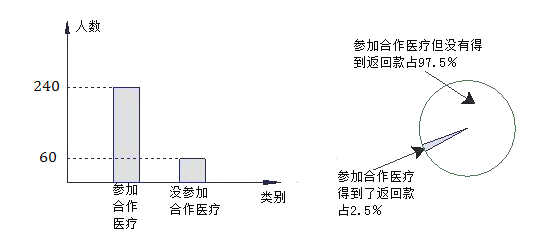
根据以上信息,解答以下问题:
(1)本次调查了______名村民,被调查的村民中,有______人参加合作医疗得到了返回款?
(2)若该乡有10000名村民,请你估计有多少人参加了合作医疗?
(3)要使两年后参加合作医疗的人数增加到9680人,假设这两年的年平均增长率相同,求年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
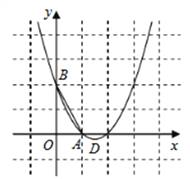
【题目】已知二次函数y=ax2+bx+c的图像如图所示,对称轴为直线x=1.有位学生写出了以下五个结论:

(1)ac>0;
(2)方程ax2+bx+c=0的两根是x1=-1,x2=3;
(3)2a-b=0;
(4)当x>1时,y随x的增大而减小;
(5)3a+2b+c>0
则以上结论中不正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图像经过点A(3,0),B(2,-3)C(0,-3)
(1)求此函数关系式和图像对称轴.
(2)在对称轴上是否存在一点P使得△PAB中PA=PB?若存在,求出点P坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形 ABCD 中,AB=3cm,动点 M 自A 点出发沿 AB 方向以每秒 1cm 的速度运动,同时点 N 自D 点出发沿折线 DC→CB 以每秒 2cm 的速度运动,到达 B 点时运动同时停止,设△AMN 的面积为 y(cm2),运动时间为 x(秒),则下列图象中能大致反映 y 与 x 之间函数关系的是( )

A.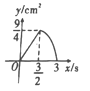 B.
B.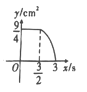 C.
C.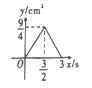 D.
D.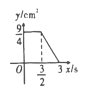
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位篮球运动员在距离篮圈中心水平距离![]() 处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为
处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为![]() 时,达到最大高度
时,达到最大高度![]() ,然后准确落入篮筐内.已知篮圈中心距离地面高度为
,然后准确落入篮筐内.已知篮圈中心距离地面高度为![]() ,在如图所示的平面直角坐标系中,下列说法正确的是( )
,在如图所示的平面直角坐标系中,下列说法正确的是( )
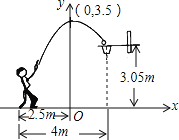
A.篮圈中心的坐标是![]()
B.此抛物线的解析式是![]()
C.此抛物线的顶点坐标是![]()
D.篮球出手时离地面的高度是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,顶点为
两点,顶点为![]() .
.
(1)求抛物线的解析式;
(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后,点
后,点![]() 落在点
落在点![]() 的位置,将抛物线沿
的位置,将抛物线沿![]() 轴平移后经过点
轴平移后经过点![]() ,求平移后所得图象的函数关系式;
,求平移后所得图象的函数关系式;
(3)设(2)中平移后,所得抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() ,若点
,若点![]() 在平移后的抛物线上,且满足
在平移后的抛物线上,且满足![]() 的面积是
的面积是![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店计划购进甲、乙两种商品,乙种商品的进价是甲种商品进价的九折,用3600元购买乙种商品要比购买甲种商品多买10件.
(1)求甲、乙两种商品的进价各是多少元?
(2)该商店计划购进甲、乙两种商品共80件,且乙种商品的数量不低于甲种商品数量的3倍.甲种商品的售价定为每件80元,乙种商品的售价定为每件70元,若甲、乙两种商品都能卖完,求该商店能获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
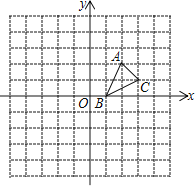
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,三个顶点的坐标分别为A(2,2)、B(1,0)、C(3,1)
(1)将△ABC关于x轴作轴对称变换得△A1B1C1,则点C1的坐标为 .
(2)将△ABC绕原点O按逆时针方向旋转90°得△A2B2C2,则点C2的坐标为 .
(3)在(1)(2)的基础上,图中的△A1B1C1、△A2B2C2是中心对称图形,对称中心的坐标为 .
(4)若以点D、A、C、B为顶点的四边形为菱形,直接写出点D的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com