
����Ŀ��2018��ȫ��������3��5����20���ڱ����ٿ���Ϊ���˽���������ȡ�������ŵ�����Ҫ;����������С�չ��һ�γ������飬���ݵ�������������ͼ��ʾ�в�������ͳ��ͼ������ͼ����Ϣ����������⣺
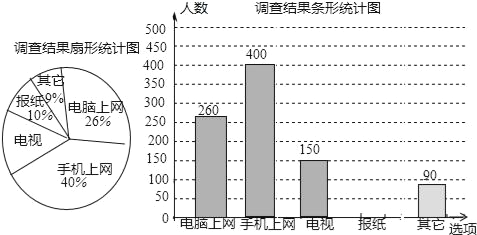
��1����ν��ܵ������������������ ����
��2������ͳ��ͼ�У�������������Ӧ��Բ�ĽǵĶ������� ����
��3���벹ȫ����ͳ��ͼ��
��4��������Լ��700���ˣ�����������н��������������ֻ���������Ϊ����ȡ���ŵ�����Ҫ;��������������
���𰸡���1��1000����2��54�㣻��3������������4��462000�ˣ�
��������
���⣨1���õ���������������ռ�İٷֱȼ������.��2�������������������Ӧ��Բ�Ľ�ռ����Բ�ܵİٷ�������Բ�ܽdz�������ٷ����������.��3������������������ֽ��ռ�İٷ����������.��4������������Ժ��ֻ�������������ռ��ε��������İٷ���������80���������ٷ����������.
�����������1��260��26%=1000�ˣ�����ν��ܵ����������������1000�ˣ���2��360����1-9%-10%-26%-40%��=360��15%=54����4��1000��10%=100�ˣ���Ӧ��ȫ����ͳ��ͼ����5�������Ժ��ֻ�������������ռ��ε��������İٷ�������260+400����1000=66%,80��66%=52.8����,���������н������Ժ��ֻ���������Ϊ����ȡ���ŵ�����Ҫ;��������������52.8����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=�� ![]() x+1��x�ᡢy��ֱ���B�㡢A�㣬ֱ��y=2x��2��x�ᡢy��ֱ���D�㡢E�㣬����ֱ�߽��ڵ�C��
x+1��x�ᡢy��ֱ���B�㡢A�㣬ֱ��y=2x��2��x�ᡢy��ֱ���D�㡢E�㣬����ֱ�߽��ڵ�C��
��1����A��B��C��D��E�����ꣻ
��2���������������ε����֪ʶ֤����AB��DE��
��3�����CBD�����Բ�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ij�������������ABCD��A��B��C��D��װ��һЩҺ�壬��ABʼ����ˮƽ�����ϣ������ײ�����б��Ϊ������CBE=������ͼ1��ʾ����̽�� ��ͼ1��Һ��պù���CD��������BB�佻�ڵ�Q����ʱҺ�����״Ϊֱ��������������ͼ���ߴ���ͼ2��ʾ��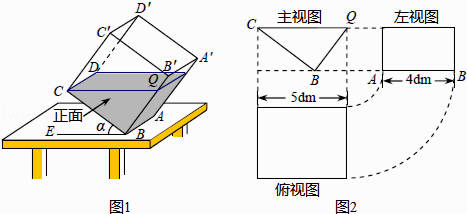
������⣺
��1��CQ��BE��λ�ù�ϵ�� �� BQ�ij���dm��
��2����Һ�����������ο��㷨��ֱ�������VҺ=�����S��BCQ����AB��
��3������Ķ�������ע��sin49��=cos41��= ![]() ��tan37��=
��tan37��= ![]() ��
��
��4�����죺��ͼ4�Ļ����ϣ��������ײ����м�λ�ã�Ƕ��һƽ���ڲ���ij����θ��壨��Ⱥ��Բ��ƣ����õ�ͼ5�������NM=1dm��BM=CM��NM��BC���������һ�����ת������=60��ʱ��ͨ�����㣬�ж����������Һ���ܷ�ﵽ4dm3 �� 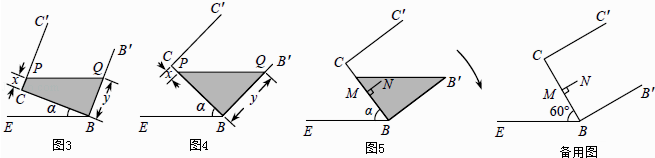
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
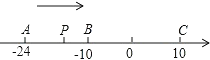
����Ŀ����֪��������A��B��C�����㣬�ֱ��ʾ��������24����10��10������P��A��������ÿ��1����λ���ٶ����յ�C�ƶ������ƶ�ʱ��Ϊt�룮
��1���ú�t�Ĵ���ʽ��ʾP����A�͵�C�ľ��룺
PA=________��PC=________��
��2������P�˶���B��ʱ����Q��A���������ÿ��3����λ���ٶ���C���˶���Q�㵽��C�����������ͬ�����ٶȷ��أ��˶����յ�A���ڵ�Q��ʼ�˶���P��Q����֮��ľ����ܷ�Ϊ2����λ������ܣ��������ʱ��P��ʾ������������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
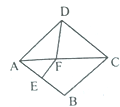
����Ŀ����ͼ��������ABCD�У���BAD=80![]() ��AB�Ĵ�ֱƽ���߽��Խ���AC�ڵ�F������Ϊ��E������DF�����CDF�Ķ�����____.
��AB�Ĵ�ֱƽ���߽��Խ���AC�ڵ�F������Ϊ��E������DF�����CDF�Ķ�����____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪ƽ���ı���ABCD���Խ���AC��BD�ཻ�ڵ�O����OBC=��OCB��
��1����֤��ƽ���ı���ABCD�Ǿ��Σ�
��2��������һ������ʹ����ABCDΪ�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������й���һ���Ľ�ħ�������������40%���ۣ�Ϊ�����������������������о�������۳��ۣ���ʱÿ��ħ�����ۼ�Ϊ28Ԫ.
��1����ħ���Ľ��ۣ�
��2����������һ������ø���˫ʮһ�������̵������ʣ�µ�ħ����ÿ3��80Ԫ�ļ۸���ۣ��ܿ�����һ�գ�����ħ�����й�����2800Ԫ����ó��й�����ħ�����ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ű�����ȫ��ͬ��ֽ��A��B��C��D�У���������ֱ����ĸ���ͬ�ļ���ͼ�Σ���ͼ����С������4��ֽ�Ʊ��泯��ϴ�Ⱥ�����һ�ţ����Żأ����ٴ����µ�3��ֽ��������һ�ţ�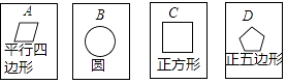
��1������״ͼ�����б�������ʾ�����������п��ܳ��ֵĽ����ֽ�ƿ���A��B��C��D��ʾ����
��2������������ֽ����������������ͼ�Σ�������Գ�ͼ���������ĶԳ�ͼ�εĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD����һ��P����AP=AB��PB=PC������AC��PD�� 
��֤��
��1����APB�ա�DPC��
��2����BAP=2��PAC��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com