
【题目】如图,已知在边长为4的菱形ABCD中,∠C=60°,E是BC边上一动点(与点B,C不重合).连接DE,作∠DEF=60°,交AB于点F,设CE=x,△FBE的面积为y.下列图象中,能大致表示y与x的函数关系的是( )
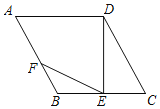
A.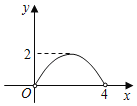 B.
B.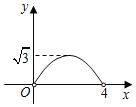
C.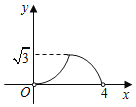 D.
D.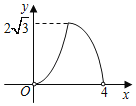
科目:初中数学 来源: 题型:
【题目】某商场为了方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式扶梯AB长为10m,坡角∠ABD=30°;改造后斜坡式自动扶梯的坡角∠ACB=9°,请计算改造后的斜坡AC的长度,(结果精确到0.01(sin9°≈0.156,cos9°≈0.988,tan9°≈0.158)
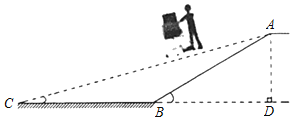
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(l,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是抛物线上的动点,且满足S△PAO=2S△PCO,求出P点的坐标;
(3)连接BC,点E是x轴一动点,点F是抛物线上一动点,若以B、C、E、F为顶点的四边形是平行四边形时,请直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时1.5秒,这辆校车是否超速?说明理由.(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
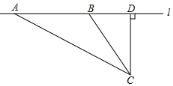
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,BA=BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.
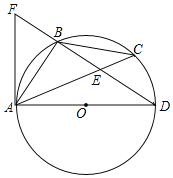
(1)求证:AF是⊙O的切线;
(2)若BC=2![]() ,BE=4,求⊙O半径r.
,BE=4,求⊙O半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
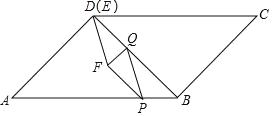
【题目】如图,BD是ABCD的对角线,AD⊥BD,AB=2![]() cm,∠A=45°.动点P从点B出发,以
cm,∠A=45°.动点P从点B出发,以![]() cm/s的速度沿BA运动到终点A,同时动点Q从点D出发,以2cm/s的速度沿折线DB﹣BC向终点C运动,当一点到达终点时另一点也停止运动.过点Q作QE⊥AD,交射线AD于点E,连接PQ,以PQ与EQ为边作PQEF.设点P的运动时间为t(s),PQEF与ABCD重叠部分图形的面积为S(cm2).
cm/s的速度沿BA运动到终点A,同时动点Q从点D出发,以2cm/s的速度沿折线DB﹣BC向终点C运动,当一点到达终点时另一点也停止运动.过点Q作QE⊥AD,交射线AD于点E,连接PQ,以PQ与EQ为边作PQEF.设点P的运动时间为t(s),PQEF与ABCD重叠部分图形的面积为S(cm2).
(1)AP= cm(用含的代数式表示);
(2)当点F落在边AD上时,求t的值:
(3)求S与t之间的函数关系式;
(4)连接FQ,当FQ所在的直线将ABCD分成面积相等的两部分时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
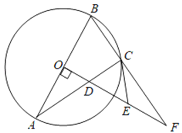
【题目】如图,△ABC内接于⊙O,AB为直径,作OD⊥AB交AC于点D,延长BC,OD交于点F,过点C作⊙O的切线CE,交OF于点E.
(1)求证:EC=ED;
(2)如果OA=4,EF=3,求弦AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com