
【题目】如图,AB为⊙O的直径,CF切⊙O于点C,BF⊥CF于点F,点D在⊙O上,CD交AB于点E,∠BCE=∠BCF.
(1)求证:弧AC=弧AD;
(2)点G在⊙O上,∠GCD=∠FCD,连接DO并延长交CG于点H,求证:CH=GH;
(3)在(2)的条件下,连接AG,AG=3,CF=2![]() ,求CG的长.
,求CG的长.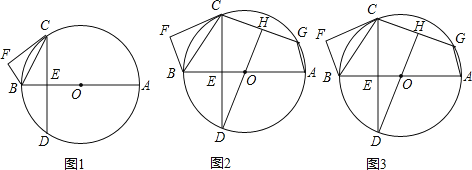
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)如图1,连接半径,根据切线的性质得出垂直,与已知BF⊥FC,得BF∥OC,所以∠BEC=∠BFC=90°,由垂径定理得:弧AC=弧AD;
(2)如图2,根据同圆半径相等得∠OCD=∠D,由切线的性质得∠FCD+∠OCD=90°,根据等量代换得:
∠DCG+∠D=90°,所以∠DHC=90°,由垂径定理得CH=HG;
(3)如图3中,延长GA到M,使得AD=AM,连接DM,延长CG到N,使得GN=GD,连接AN,作DJ⊥AM于J.首先证明△CAD≌△MAD,得AM=AC,DM=CD=DG,同理可得GN=DG,AN=AD=AC,再证明DM2-DA2=(DJ2+JM2)-(DJ2+AJ2)=(JM+AJ)(JM-AJ)=AMAG,求出AD,同理可得AN2-AG2=GNCG,延长即可解决问题.
证明:(1)如图1,连接OC,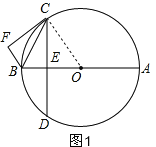
∵OC=OB,
∴∠OBC=∠OCB,
∵FC是⊙O的切线,
∴OC⊥FC,
∵BF⊥FC,
∴BF∥OC,∠BFC=90°,
∴∠OCB=∠FBC,
∴∠OBC=∠FBC,
∵∠BCE=∠BCF,
∴△FBC∽△EBC,
∴∠BEC=∠BFC=90°,
∴OB⊥DC,
∴弧AC=弧AD;
(2)如图2,连接OC.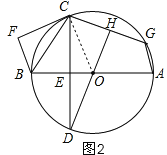
∵OC=OD,
∴∠OCD=∠D,
∵FC是⊙O的切线,
∴∠FCD+∠OCD=90°,
∵∠FCD=∠DCG,
∴∠DCG+∠D=90°,
∴∠DHC=90°,
∴DH⊥CG,
∵DH经过圆心O,
∴CH=HG.
(3)如图3中,延长GA到M,使得AD=AM,连接DM,延长CG到N,使得GN=GD,连接AN,作DJ⊥AM于J.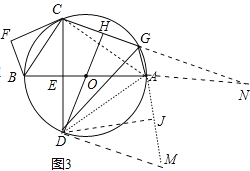
∵CE=CF=2![]() ,
,
∴CD=2![]() ,
,
∵DC=DG,AC=AD,
∵∠DAM=∠DCG=∠CAD,
∴△CAD≌△MAD,
∴AM=AC,DM=CD=DG,
同理可证GN=DG,AN=AD=AC,
∵DM2-DA2=(DJ2+JM2)-(DJ2+AJ2)=(JM+AJ)(JM-AJ)=AMAG,
∴(4![]() )2-AD2=AD3,
)2-AD2=AD3,
解得AD=13,
同理在等腰三角形△NAC中可得AN2-AG2=GNCG,
∴169-9=4![]() CG,∴CG=
CG,∴CG=![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,过原点的直线与反比例函数![]() (k>0)的图象交于A,B两点,点A在第一象限点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为____.
(k>0)的图象交于A,B两点,点A在第一象限点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
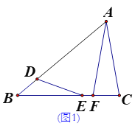
【题目】△ABC中,∠BAC=60°,点D在AB上,点E,F在BC上,∠ADE=60°,∠BAF=2∠BED.
(1)如图1,求证:AF=AC;
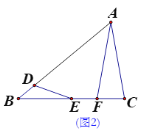
(2)如图2,当E为BC的中点时,求证:AD-BD=AF;
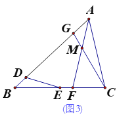
(3)如图3,在(2)的条件下,在AB上取点G,使∠ACG=∠BED,连接CG交AF于点M,若BD=3,FM=8,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB上的一点,连接CD,CE∥AB,BE∥CD,且CE=AD.
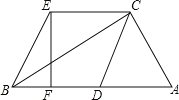
(1)求证:四边形BDCE是菱形;
(2)过点E作EF⊥BD,垂足为点F,若点F是BD的中点,EB=6,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴相交于A.B两点,点A在点B左侧,顶点在折线M﹣P﹣N上移动,它们的坐标分别为M(﹣1,4).P(3,4).N(3,1).若在抛物线移动过程中,点A横坐标的最小值为﹣3.则a﹣b+c的最小值是( )
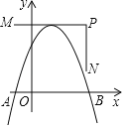
A.﹣15B.﹣12C.﹣4D.﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+5与x轴交于A(﹣1,0),B(5,0)两点(点A在点B的左侧),与y轴交于点C.
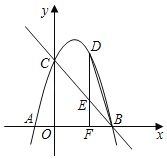
(1)求抛物线的解析式;
(2)点D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.
(3)若M为抛物线对称轴上一动点,使得△MBC为直角三角形,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为10元,试销过程中发现,每月销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系可以近似地看作一次函数,且当
(元)之间的关系可以近似地看作一次函数,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求出销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)若每月的利润为![]() (万元),求出利润
(万元),求出利润![]() (万元)与销售单价
(万元)与销售单价![]() (元)的函数关系式?当销售单价为多少元时,厂商每月能获得的利润
(元)的函数关系式?当销售单价为多少元时,厂商每月能获得的利润![]() 最大?
最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泉州市旅游资源丰富,①清源山、②开元寺、③崇武古城三个景区是人们节假日玩的热点景区,张老师对八(1)班学生“五·一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别:A、游三个景区;B,游两个景区;C,游一个景区:D,不到这三个景区游玩现根据调查结果绘制了不完整的条形统计图和廟形统计图,请结合图中信息解答下列问题:
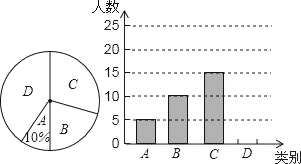
(1)八(1)班共有学生 人在扇形统计图中,表示“B类别的扇形的圆心角的度数为 ;
(2)请将条形统计图补充完整;
(3)若小华、小刚两名同学,各自从三个最区中随机选一个作为5月1日游玩的景区,请用树状图或列表法求他们选中同个景区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com