
【题目】某电子厂商投产一种新型电子产品,每件制造成本为10元,试销过程中发现,每月销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系可以近似地看作一次函数,且当
(元)之间的关系可以近似地看作一次函数,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求出销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)若每月的利润为![]() (万元),求出利润
(万元),求出利润![]() (万元)与销售单价
(万元)与销售单价![]() (元)的函数关系式?当销售单价为多少元时,厂商每月能获得的利润
(元)的函数关系式?当销售单价为多少元时,厂商每月能获得的利润![]() 最大?
最大?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,CF切⊙O于点C,BF⊥CF于点F,点D在⊙O上,CD交AB于点E,∠BCE=∠BCF.
(1)求证:弧AC=弧AD;
(2)点G在⊙O上,∠GCD=∠FCD,连接DO并延长交CG于点H,求证:CH=GH;
(3)在(2)的条件下,连接AG,AG=3,CF=2![]() ,求CG的长.
,求CG的长.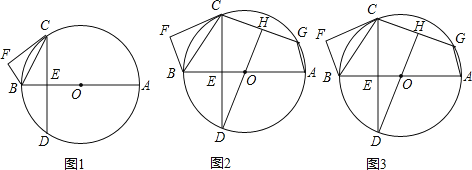
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转后,得到△ADF,此时点D落在边BC的中点处,则图中与∠C相等的角(除∠C外)有( )

A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的二次函数![]() 与x轴有交点.若关于x的一元二次方程
与x轴有交点.若关于x的一元二次方程![]() 的两根分别是
的两根分别是![]() ,
,![]() 。
。
(1)求二次函数的解析式;
(2)设A(a,c)和B(b,c)是抛物线上两点,且AB=4,a<b,求a、b、c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )

A. 小球的飞行高度不能达到15m
B. 小球的飞行高度可以达到25m
C. 小球从飞出到落地要用时4s
D. 小球飞出1s时的飞行高度为10m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的一角![]() 两边为边,用总长为
两边为边,用总长为![]() 的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且这三块区域的面积相等,四边形
的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且这三块区域的面积相等,四边形![]() 为直角梯形.
为直角梯形.
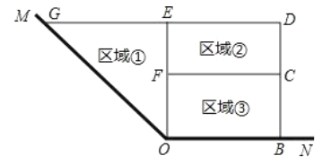
(1)设![]() 的长度为
的长度为![]() ,则
,则![]() 的长为______
的长为______![]() ;
;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并注明自变量
之间的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(3)![]() 为何值时,
为何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别写有数字1,2,3的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求:
(1)两次取出小球上的数字相同的概率;
(2)两次取出小球上的数字之和大于3的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com