
����Ŀ����ͼ����֪������y��ax2+bx+5��x�ύ��A����1��0����B��5��0�����㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
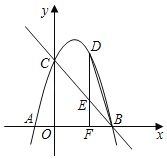
��1���������ߵĽ���ʽ��
��2����D�ǵ�һ�������������ϵ�һ�����㣨���C��B���غϣ�������D��DF��x���ڵ�F����ֱ��BC�ڵ�E������BD��ֱ��BC�ܷ�ѡ�BDF�ֳ����֮��Ϊ2��3�������֣����ܣ��������D�����ꣻ�����ܣ���˵�����ɣ�
��3����MΪ�����߶Գ�����һ���㣬ʹ�á�MBCΪֱ�������Σ���ֱ��д����M�����꣮
���𰸡���1��y����x2+4x+5����2������D������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ��ʱ��ֱ��BC�ѡ�BDF�ֳ����֮��Ϊ2��3�������֣���3������������M�������Ϊ��2��7������2����3������2��6������2����1����
��ʱ��ֱ��BC�ѡ�BDF�ֳ����֮��Ϊ2��3�������֣���3������������M�������Ϊ��2��7������2����3������2��6������2����1����
��������
��1������������x���������������������ʽ���г���Ԫһ�η�����![]() ����˷����鼴����������ߵĽ���ʽ��
����˷����鼴����������ߵĽ���ʽ��
��2�����ͼ���֪��BDE�͡�BEF�ǵȸߵ������ɴ˵ó����ǵ�����ȼ�ΪDE��EF��2��3��������������������������ľ��빫ʽ���ɵó����̣��ⷽ�����D�����ꣻ
��3�������������MBCΪֱ��������ʱM�����꼴��.
��1����A����1��0����B��5��0������y��ax2+bx+5��
�ã�![]() ��
��
���![]() ��
��
�������߽���ʽΪy����x2+4x+5��
��2���ܣ�
��ֱ��BC�Ľ���ʽΪy��kx+b��
��C��0��5����B��5��0�������![]()
![]() ��
��
���![]() ��
��
����ֱ��BC�Ľ���ʽΪy����x+5��
��D��x����x2+4x+5������E��x����x+5����F��x��0������0��x��5����
��DE����x2+4x+5������x+5������x2+5x��EF����x+5��
��DE��EF��2��3ʱ��S��BDE��S��BEF��2��3��
������x2+5x��������x+5����2��3��
������3x2��17x+10��0��
���x1��![]() ��x2��5����ȥ������ʱD������Ϊ��
��x2��5����ȥ������ʱD������Ϊ��![]() ��
��![]() ����
����
��DE��EF��3��2ʱ��S��BDE��S��BEF��3��2��������x2+5x��������x+5����3��
������2x2��13x+15��0��
���x1��![]() ��x2��5����ȥ������ʱD������Ϊ��
��x2��5����ȥ������ʱD������Ϊ��![]() ��
��![]() ����
����
��������������D��������![]() ��
��![]() ����
����![]() ��
��![]() ��ʱ��ֱ��BC�ѡ�BDF�ֳ����֮��Ϊ2��3�������֣�
��ʱ��ֱ��BC�ѡ�BDF�ֳ����֮��Ϊ2��3�������֣�
��3�������ߵĶԳ���Ϊֱ��x��2����ͼ��

��M��2��t����
��B��5��0����C��0��5����
��BC2��52+52��50��MC2��22+��t��5��2��t2��10t+29��MB2����2��5��2+t2��t2+9��
��BC2+MC2��MB2ʱ����BCMΪֱ�������Σ���BCM��90������50+t2��10t+29��t2+9�����t��7����ʱM�������Ϊ��2��7����
��BC2+MB2��MC2ʱ����BCMΪֱ�������Σ���CBM��90������50+t2+9��t2��10t+29�����t����3����ʱM�������Ϊ��2����3����
��MC2+MB2��BC2ʱ����BCMΪֱ�������Σ���CMB��90������t2��10t+29+t2+9��50�����t1��6��t2����1����ʱM�������Ϊ��2��6����2����1����
��������������������M���������2��7������2����3������2��6������2����1����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڰ뾶����5 cm��Բ���г�Ϊ![]() cm���ң���������Ե�Բ�ܽ�Ϊ
cm���ң���������Ե�Բ�ܽ�Ϊ
A.60��B.120��C.60���120��D.30���120��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B��D��F��AN�ϣ�C��E��AM�ϣ���AB=BC=CD=ED=EF����A=20�������FEB= __________
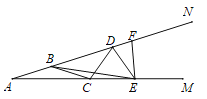
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����CF�С�O�ڵ�C��BF��CF�ڵ�F����D�ڡ�O�ϣ�CD��AB�ڵ�E����BCE=��BCF��
��1����֤����AC=��AD��
��2����G�ڡ�O�ϣ���GCD=��FCD������DO���ӳ���CG�ڵ�H����֤��CH=GH��
��3���ڣ�2���������£�����AG��AG=3��CF=2![]() ����CG�ij���
����CG�ij���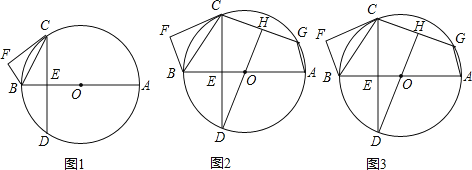
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OAB�У���ABO��90������Aλ�ڵ�һ���ޣ���OΪ����ԭ�㣬��B��x���������ϣ���˫����y��![]() ��x��0�����OAB�ı�AO.AB�ֱ��ڵ�C.D����CΪAO���е㣬����OD.CD����S��OBD��3����S��OCDΪ_____��
��x��0�����OAB�ı�AO.AB�ֱ��ڵ�C.D����CΪAO���е㣬����OD.CD����S��OBD��3����S��OCDΪ_____��
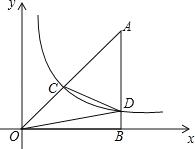
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BAC=90��������ABC�Ƶ�A˳ʱ����ת�õ���ADF����ʱ��D���ڱ�BC���е㴦����ͼ������C��ȵĽǣ�����C�⣩�У� ��

A��5�� B��4�� C��3�� D��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�Ķ��κ���![]() ��x���н��㣮������x��һԪ���η���
��x���н��㣮������x��һԪ���η���![]() �������ֱ���
�������ֱ���![]() ��
��![]() ��
��
��1������κ����Ľ���ʽ��
��2����A(a,c)��B��b,c���������������㣬��AB=4,a<b����a��b��c��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ʡ���ϣ�ijˮ����ֳ������ˮ���һ��![]() ����Ϊ�ߣ����ܳ�Ϊ
����Ϊ�ߣ����ܳ�Ϊ![]() ��Χ����ˮ����Χ������ͼ��ʾ�Ģ٢ڢ������������������Ϊֱ�������Σ�����ڢ�Ϊ���Σ���������������������ȣ��ı���
��Χ����ˮ����Χ������ͼ��ʾ�Ģ٢ڢ������������������Ϊֱ�������Σ�����ڢ�Ϊ���Σ���������������������ȣ��ı���![]() Ϊֱ������.
Ϊֱ������.
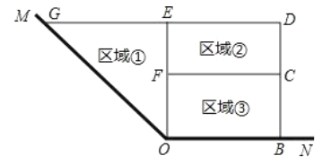
��1����![]() �ij���Ϊ
�ij���Ϊ![]() ����
����![]() �ij�Ϊ______
�ij�Ϊ______![]() ��
��
��2�����ı���![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ����ע���Ա���
֮��ĺ�����ϵʽ����ע���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() �����ֵ�����ֵ�Ƕ��٣�
�����ֵ�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ACB��90����AC��6cm��BC��8cm������P�ӵ�B��������BA������ÿ��5cm���ٶ����A�����˶���ͬʱ����Q�ӵ�C��������CB������ÿ��4cm���ٶ����B�����˶����˶�ʱ��Ϊt�루0��t��2��������PQ��

��1������BPQ����ABC���ƣ���t��ֵ��
��2����̽��tΪ��ֵʱ����BPQ�������![]() cm2��
cm2��
��3��ֱ��д��tΪ��ֵʱ����BPQ�ǵ��������Σ�
��4������AQ��CP����AQ��CP��ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com