
【题目】△ABC中,∠BAC=60°,点D在AB上,点E,F在BC上,∠ADE=60°,∠BAF=2∠BED.
(1)如图1,求证:AF=AC;
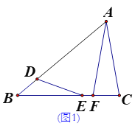
(2)如图2,当E为BC的中点时,求证:AD-BD=AF;
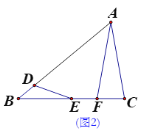
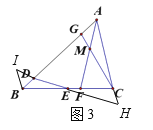
(3)如图3,在(2)的条件下,在AB上取点G,使∠ACG=∠BED,连接CG交AF于点M,若BD=3,FM=8,求AD的长.
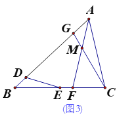
【答案】(1)见解析;(2)见解析;(3)AD=17
【解析】
(1)利用三角形内角和公式用∠B表示∠C,再用三角形外角性质用∠BAF和∠B表示∠AFC,最后化简后得到∠C=∠AFC,即可证到AF=AC.
(2)利用旋转后三角形全等,证出△CGH和△ADH是等边三角形,BD=CG=CH,由(1)得出的结论即可证出AD-BD=AF.
(3)设AM=x过点B作直线BI平行与AC,得到△IBE≌△HCE,∠IBE=∠HCE,再由∠BAC=∠I,∠ACG=∠BED,得到△IBE∽△AGC,∠IBE=∠AGC,![]() ,再证得△ABF∽△AMB,得
,再证得△ABF∽△AMB,得![]() ,通过以上两个比例解出AM的值,再求出AD的值.
,通过以上两个比例解出AM的值,再求出AD的值.
解:(1)∠C=180°-∠BAC-∠B=120°-∠B,
∠AFC=∠BAF+∠B =2∠BED+∠B=2(∠ADE-∠B)+∠B=120°-∠B,
∴∠C=∠AFC,
∴AF=AC.
(2)如图2所示:旋转△BDE,使B与C重合,得△CGE,延长AC、DG交于点H.
由(1)得∠ACB=120°-∠B.
又∵∠ECG=∠B,
∴∠ACG=∠ACB+∠ECG=120°-∠B+∠B=120°,
∴∠GCH=60°,
又∵∠BDE=∠CGE=120°,
∴∠CGH=60°,
∴∠GCH=∠CGH,
∴△CGH是等边三角形,
∴∠H=60°,且BD=CG=CH,
又∵∠ADE=60°,
∴△ADH是等边三角形,
∴AD=AH=AC+CH=AC+BD=AF+BD,
∴AD-BD=AF.
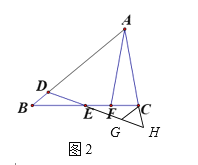
(3)如图3所示,延长DE、AC交于点H,过点B作BI∥AC交DE于点I,设AM=x,
则有AF=AC=8+x,
∵∠BAC=60°,∠ADE=60°,
∴△ADH是等边三角形,
∴AD=AC=DH,∠H=60°,
又∵BI∥AC,
∴△BID也是等边三角形,
∴BI=BD=DI=3,∠I=∠IBD=∠IDB=60°.
∵∠I=∠H=60°,∠IEB=∠HEC,BE=CE,
∴△IBE≌△HCE,
∴IE=HE,IB=HC=3,∠IBE=∠HCE,
∴AD=AC=DH=AC+HC=11+x,
∴EI=![]() HI=
HI=![]() (11+x+3)=
(11+x+3)=![]() (14+x).
(14+x).
∵∠BAC=∠I=60°,∠ACG=∠BED,
∴△IBE∽△AGC,
∴∠IBE=∠AGC,![]() ,
,
∴∠HCE=∠AGC,
又∵∠ACF=∠AFC,
∴∠HCE=∠AFB=∠AGC,
∵∠AFB=∠AGC,∠GAM=∠GAM,
∴△ABF∽△AMB,
∴![]() ,
,
由![]() ,
,![]() ,得:
,得:
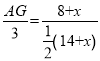 ,
,![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
∴AM=6,
∴AD=17.


科目:初中数学 来源: 题型:
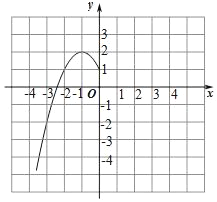
【题目】某班“数学兴趣小组”对函数y=﹣x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣2 | ﹣ | m | 2 | 1 | 2 | 1 | ﹣ | ﹣2 | … |
其中,m= .
(2)根据上表数据,在如图所示的平面直角坐标系中描点,画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①方程﹣x2+2|x|+1=0有 个实数根;
②关于x的方程﹣x2+2|x|+1=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划利用一片空地建一个学生自行车车棚,自行车车棚为矩形,其中一面靠墙,这堵墙的长度为![]() ,另三面墙用现有的木板材料围成,总长为
,另三面墙用现有的木板材料围成,总长为![]() ,且计划建造车棚的面积为
,且计划建造车棚的面积为![]()
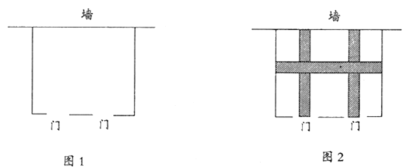
(1)如图1,为了方便学生出行,学校决定在与墙平行的一面留两个![]() 宽的门,求这个车棚的长和宽;
宽的门,求这个车棚的长和宽;
(2)如图2,为了方使学生停取车,施工单位又决定在车棚内修建一条平行于墙和两条垂直于墙的![]() 条等宽小路,使得剩余面积为
条等宽小路,使得剩余面积为![]() ,求小路的宽度。
,求小路的宽度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,CF切⊙O于点C,BF⊥CF于点F,点D在⊙O上,CD交AB于点E,∠BCE=∠BCF.
(1)求证:弧AC=弧AD;
(2)点G在⊙O上,∠GCD=∠FCD,连接DO并延长交CG于点H,求证:CH=GH;
(3)在(2)的条件下,连接AG,AG=3,CF=2![]() ,求CG的长.
,求CG的长.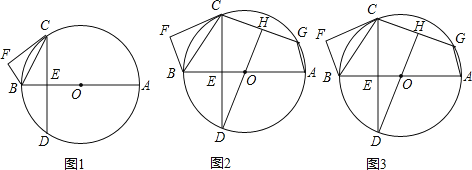
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转后,得到△ADF,此时点D落在边BC的中点处,则图中与∠C相等的角(除∠C外)有( )

A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别写有数字1,2,3的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求:
(1)两次取出小球上的数字相同的概率;
(2)两次取出小球上的数字之和大于3的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com