
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
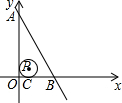 如图,直线y=-$\sqrt{3}x+4\sqrt{3}$与x,y轴分别交于点B、A两点,⊙P的圆心坐标为(1,1),且与x轴相切于点C,现将⊙P从如图所示的位置开始沿x轴向右滚动,当⊙P与直线AB相切时,圆心P运动的距离为3-$\sqrt{3}$或3+$\frac{\sqrt{3}}{3}$.
如图,直线y=-$\sqrt{3}x+4\sqrt{3}$与x,y轴分别交于点B、A两点,⊙P的圆心坐标为(1,1),且与x轴相切于点C,现将⊙P从如图所示的位置开始沿x轴向右滚动,当⊙P与直线AB相切时,圆心P运动的距离为3-$\sqrt{3}$或3+$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某供电公司,为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的图象如图所示.
某供电公司,为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑方二百步,各中开门.出东门一五步有木.问出南门几何步而见木?”译文:“今有正方形小城边长为200步,各方中央开一城门.走出东门15步处有树,问出南门多少步能见到树?”请你结合题意画出图形,并完成求解.
《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑方二百步,各中开门.出东门一五步有木.问出南门几何步而见木?”译文:“今有正方形小城边长为200步,各方中央开一城门.走出东门15步处有树,问出南门多少步能见到树?”请你结合题意画出图形,并完成求解.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com