
 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑方二百步,各中开门.出东门一五步有木.问出南门几何步而见木?”译文:“今有正方形小城边长为200步,各方中央开一城门.走出东门15步处有树,问出南门多少步能见到树?”请你结合题意画出图形,并完成求解.
《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑方二百步,各中开门.出东门一五步有木.问出南门几何步而见木?”译文:“今有正方形小城边长为200步,各方中央开一城门.走出东门15步处有树,问出南门多少步能见到树?”请你结合题意画出图形,并完成求解. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$÷(-4)=4×(-4) | B. | -5÷(-$\frac{1}{2}$)=-5×(-2) | C. | 7-(-3)=7+3 | D. | 6-7=(+6)+(-7) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
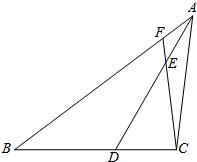 已知:如图,△ABC中,AD平分∠BAC交BC于点D,且∠ADC=60°,若∠ACB为钝角,且AB>AC,BD>DC.
已知:如图,△ABC中,AD平分∠BAC交BC于点D,且∠ADC=60°,若∠ACB为钝角,且AB>AC,BD>DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有这样一个问题:探究函数y=$\frac{1}{{{x^2}-1}}$的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{{{x^2}-1}}$的图象与性质.| x | … | -$\frac{9}{4}$ | -2 | -$\frac{7}{4}$ | -$\frac{3}{2}$ | -$\frac{5}{4}$ | … |
| y | … | 0.25 | 0.33 | 0.48 | 0.8 | 1.78 | … |
| x | -$\frac{3}{4}$ | -$\frac{1}{2}$ | $\frac{1}{4}$ | 0 | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{3}{4}$ |
| y | -2.29 | -1.33 | -1.07 | -1 | -1.07 | -1.33 | -2.29 |
| x | … | $\frac{5}{4}$ | $\frac{3}{2}$ | $\frac{7}{4}$ | 2 | $\frac{9}{4}$ | … |
| y | … | 1.78 | 0.8 | 0.48 | 0.33 | 0.25 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com