
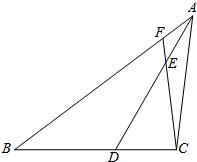
 已知:如图,△ABC中,AD平分∠BAC交BC于点D,且∠ADC=60°,若∠ACB为钝角,且AB>AC,BD>DC.
已知:如图,△ABC中,AD平分∠BAC交BC于点D,且∠ADC=60°,若∠ACB为钝角,且AB>AC,BD>DC.分析 (1)利用全等三角形的判定与性质得出△AGD≌△ACD(SAS),进而得出DG=DC,再利用三角形三边关系得出答案;
(2)利用全等三角形的判定与性质得出△BGD≌△ECD,进而得出,∠BFC=180°-∠B-∠7=180°-∠6-∠7即可得出答案.
解答 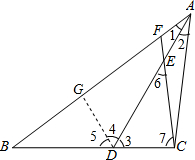 (1)证明:在AB上截取AG,使AG=AC,连接GD.(如图)
(1)证明:在AB上截取AG,使AG=AC,连接GD.(如图)
∵AD平分∠BAC,
∴∠1=∠2.
在△AGD和△ACD中,
$\left\{\begin{array}{l}{AG=AC}\\{∠1=∠2}\\{AD=AD}\end{array}\right.$,
∴△AGD≌△ACD(SAS).
∴DG=DC.
∵△BGD中,BD-DG<BG,
∴BD-DC<BG.
∵BG=AB-AG=AB-AC,
∴BD-DC<AB-AC;
(2)解:∵由(1)知△AGD≌△ACD,
∴GD=CD,∠4=∠3=60°.
∴∠5=180°-∠3-∠4=180°-60°-60°=60°.
∴∠5=∠3.
在△BGD和△ECD中,
$\left\{\begin{array}{l}{DB=DE}\\{∠5=∠3}\\{DG=DC}\end{array}\right.$,
∴△BGD≌△ECD(SAS).
∴∠B=∠6.
∵△BFC中,∠BFC=180°-∠B-∠7=180°-∠6-∠7=∠3,
∴∠BFC=60°.
点评 此题主要考查了全等三角形的判定与性质以及三角形三边关系,正确得出全等三角形是解题关键.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:填空题
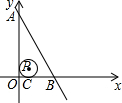 如图,直线y=-$\sqrt{3}x+4\sqrt{3}$与x,y轴分别交于点B、A两点,⊙P的圆心坐标为(1,1),且与x轴相切于点C,现将⊙P从如图所示的位置开始沿x轴向右滚动,当⊙P与直线AB相切时,圆心P运动的距离为3-$\sqrt{3}$或3+$\frac{\sqrt{3}}{3}$.
如图,直线y=-$\sqrt{3}x+4\sqrt{3}$与x,y轴分别交于点B、A两点,⊙P的圆心坐标为(1,1),且与x轴相切于点C,现将⊙P从如图所示的位置开始沿x轴向右滚动,当⊙P与直线AB相切时,圆心P运动的距离为3-$\sqrt{3}$或3+$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三角形的外角等于与它不相邻的两个内角的和 | |
| B. | 有一个角为60°的等腰三角形是等边三角形 | |
| C. | 线段垂直平分线上的点到线段两端的距离相等 | |
| D. | 等腰三角形的中线与高重合 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
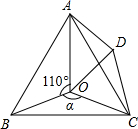 如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,
如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑方二百步,各中开门.出东门一五步有木.问出南门几何步而见木?”译文:“今有正方形小城边长为200步,各方中央开一城门.走出东门15步处有树,问出南门多少步能见到树?”请你结合题意画出图形,并完成求解.
《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑方二百步,各中开门.出东门一五步有木.问出南门几何步而见木?”译文:“今有正方形小城边长为200步,各方中央开一城门.走出东门15步处有树,问出南门多少步能见到树?”请你结合题意画出图形,并完成求解.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值.
如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com