练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．判断抛物线y=x2-4x-5是否与x轴有交点，有几个交点，请写出交点坐标，若有两个交点请求出两交点之间的距离．

    分析 根据△＞0，即可判定该抛物线与x轴一定有两个交点，解方程x2-4x-5=0，即可求得x的值，得到交点坐标及两交点之间的距离．

    解答 解：若抛物线与x轴有交点，则y=x2-4x-5=0；
    ∵△=b2-4ac=（-4）2-4×1×（-5）=36＞0
    ∴$x=\frac{{-b±\sqrt{{b^2}-4ac}}}{2a}=\frac{4±6}{2}=2±3$，
    ∴抛物线与x轴有两个交点，两个交点的横坐标为-1和5，交点坐标为（-1，0）、（5，0）．
    故两交点距离为|-1-5|=6．

    点评 本题主要考查了抛物线与x轴交点的知识，解答本题的关键是熟练掌握二次函数的性质以及顶点坐标的求法，此题难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．如图，AB=16cm，延长AB到C，使BC=3AB，D是BC的中点，求AD的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知数轴上三点A，O，B对应的数分别为-5，0，1，点M为数轴上任意一点，其对应的数为x．
    请回答问题：

    （1）A、B两点间的距离是6，若点M到点A、点B的距离相等，那么x的值是-2；
    （2）若点A先沿着数轴向右移动6个单位长度，再向左移动4个单位长度后所对应的数字是-3；
    （3）当x为何值时，点M到点A、点B的距离之和是8；
    （4）如果点M以每秒3个单位长度的速度从点O向左运动时，点A和点B分别以每秒1个单位长度和每秒4个单位长度的速度也向左运动，且三点同时出发，那么几秒种后点M运动到点A、点B之间，且点M到点A、点B的距离相等？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．（1）（x-2）（x2+4）
    （2）（0.25a2b-$\frac{1}{2}$a3b2-$\frac{1}{6}$a4b3）÷（-0.5a2b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．实数a和b在数轴上的位置如图所示，试比较5-3a与5-3b的大小关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E．
    （1）求证：BE=EC．
    （2）填空：①若∠B=30°，AC=2$\sqrt{3}$，则DE=3；
    ②当∠B=45°时，以O，D，E，C为顶点的四边形是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中卷第九勾股，主要讲述了以测量问题为中心的直角三角形三边互求的关系．其中记载：“今有邑方二百步，各中开门．出东门一五步有木．问出南门几何步而见木？”译文：“今有正方形小城边长为200步，各方中央开一城门．走出东门15步处有树，问出南门多少步能见到树？”请你结合题意画出图形，并完成求解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

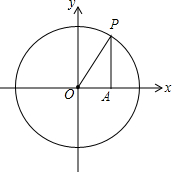    14．如图，动点P沿着半径为1的单位圆绕原点旋转，线段OP在x轴的投影为OA．
    （1）写出三角形OAP的面积y与动点P的横坐标x的关系式；
    （2）当α等于多少时，y的值最大？
    （3）写出y为最大值时，动点P的坐标．
    （提示：求y=-2x2+x的最小值，令m=x2，则：y=-2m+m2，当m=-$\frac{b}{2a}$=$\frac{2}{2}$=1时，ymin=$\frac{4ac-{b}^{2}}{4a}$=$\frac{-4}{4}$=-1，此时，x=±1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知一次函数图象过点A（2，-1），B（0，3），求该一次函数解析式．

    查看答案和解析>>

    同步练习册答案