Question

10．如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E．
（1）求证：BE=EC．
（2）填空：①若∠B=30°，AC=2$\sqrt{3}$，则DE=3；
②当∠B=45°时，以O，D，E，C为顶点的四边形是正方形．

Answer 1

分析 （1）证出EC为⊙O的切线；由切线长定理得出EC=ED，再求得EB=ED，即可得出结论；
（2）①由含30°角的直角三角形的性质得出AB，由勾股定理求出BC，再由直角三角形斜边上的中线性质即可得出DE；
②由等腰三角形的性质，得到∠ODA=∠A=45°，于是∠DOC=90°然后根据有一组邻边相等的矩形是正方形，即可得到结论．

解答 （1）证明：连接DO；如图所示：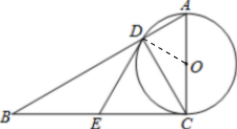
∵∠ACB=90°，AC为直径，
∴EC为⊙O的切线；
又∵ED也为⊙O的切线，
∴EC=ED，
又∵∠EDO=90°，
∴∠BDE+∠ADO=90°，
∴∠BDE+∠A=90°
又∵∠B+∠A=90°，
∴∠BDE=∠B，
∴BE=ED，
∴BE=EC；
（2）解：①∵∠ACB=90°，∠B=30°，AC=2$\sqrt{3}$，
∴AB=2AC=4$\sqrt{3}$，
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=6，
∵AC为直径，
∴∠BDC=∠ADC=90°，
由（1）得：BE=EC，
∴DE=$\frac{1}{2}$BC=3，
故答案为：3；
②当∠B=45°时，四边形ODEC是正方形，理由如下：
∵∠ACB=90°，
∴∠A=45°，
∵OA=OD，
∴∠ADO=45°，
∴∠AOD=90°，
∴∠DOC=90°，
∵∠ODE=90°，
∴四边形DECO是矩形，
∵OD=OC，
∴矩形DECO是正方形．
故答案为：45．

点评 本题考查了圆的切线性质、解直角三角形的知识、切线长定理．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．