

分析 (1)表示出阴影部分的边长,即可得出其面积;
(2)大正方形的面积减去矩形的面积即可得出阴影部分的面积,也可得出三个代数式(m+n)2、(m-n)2、mn之间的等量关系.
(3)根据(2)所得出的关系式,可求出(x-y)2,继而可得出x-y的值.
解答 解:(1)图2中的阴影部分的面积为(m-n)2.
故答案为:(m-n)2;
(2)代数式(m+n)2、(m-n)2、mn之间的等量关系式:(m+n)2-4mn=(m-n)2.
故答案为:(m+n)2-4mn=(m-n)2;
(3)(x-y)2=(x+y)2-4xy=16,
则x-y=±4.
故答案为:±4.
点评 本题考查了完全平方公式的几何背景,属于基础题,注意仔细观察图形,表示出各图形的面积是关键.


科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.
小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.| A. | 角的内部到角的两边的距离相等的点在角的平分线上 | |
| B. | 角平分线上的点到这个角两边的距离相等 | |
| C. | 三角形三条角平分线的交点到三条边的距离相等 | |
| D. | 以上均不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
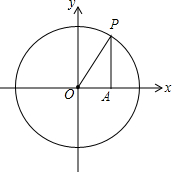 如图,动点P沿着半径为1的单位圆绕原点旋转,线段OP在x轴的投影为OA.
如图,动点P沿着半径为1的单位圆绕原点旋转,线段OP在x轴的投影为OA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,对角线BD=4$\sqrt{3}$,∠ABC=60°,对角线AC、BD交于点O,以点B为圆心,BC为半径作圆与BD交于点E,则图中阴影部分的面积为$\frac{4π}{3}$-2$\sqrt{3}$.
如图,在菱形ABCD中,对角线BD=4$\sqrt{3}$,∠ABC=60°,对角线AC、BD交于点O,以点B为圆心,BC为半径作圆与BD交于点E,则图中阴影部分的面积为$\frac{4π}{3}$-2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com