
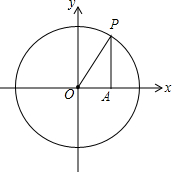
 如图,动点P沿着半径为1的单位圆绕原点旋转,线段OP在x轴的投影为OA.
如图,动点P沿着半径为1的单位圆绕原点旋转,线段OP在x轴的投影为OA.分析 (1)设动点P的横坐标为x,则OA=|x|,则利用勾股定理表述计算出PA=$\sqrt{1-{x}^{2}}$,利用三角形面积公式得到y=$\frac{1}{2}$•|x|•$\sqrt{1-{x}^{2}}$(-1≤x≤1);
(2)利用不等式公式得到|x|•$\sqrt{1-{x}^{2}}$≤$\frac{{x}^{2}+(\sqrt{1-{x}^{2}})^{2}}{2}$=$\frac{1}{2}$,则y≤$\frac{1}{4}$,由于当且仅当|x|=$\sqrt{1-{x}^{2}}$时等号成立,解关于x的方程得到x=±$\frac{\sqrt{2}}{2}$,此时y的值最大,利用特殊角的三角函数值可得OP与x轴的正方向的夹角为45°或135°;
(3)分类讨论:当OP与x轴的正方向的夹角为45°时,易得P点坐标为($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)或($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$);当OP与x轴的正方向的夹角为135°时,易得P点坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)或(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
解答 解:(1)设动点P的横坐标为x,则OA=|x|,
在Rt△OAP中,PA=$\sqrt{O{P}^{2}-O{A}^{2}}$=$\sqrt{1-{x}^{2}}$,
所以y=$\frac{1}{2}$•|x|•$\sqrt{1-{x}^{2}}$(-1≤x≤1);
(2)∵|x|•$\sqrt{1-{x}^{2}}$≤$\frac{{x}^{2}+(\sqrt{1-{x}^{2}})^{2}}{2}$=$\frac{1}{2}$,
∴y≤$\frac{1}{4}$,
∵当且仅当|x|=$\sqrt{1-{x}^{2}}$时等号成立,
∴x=±$\frac{\sqrt{2}}{2}$时,y的值最大,
此时OP与x轴的正方向的夹角为45°或135°;
即α=45°或135°时,y的值最大;
(3)当OP与x轴的正方向的夹角为45°时,P点坐标为($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)或($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$);
当OP与x轴的正方向的夹角为135°时,P点坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)或(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
点评 本题考查了圆的综合题:熟练掌握与圆有关的性质;会利用勾股定理计算相应线段的长;理解坐标与图形性质;会应用不等式公式ab≤$\frac{{a}^{2}+{b}^{2}}{2}$(a、b为正数,当且仅当a=b时取等号).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有这样一个问题:探究函数y=$\frac{1}{{{x^2}-1}}$的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{{{x^2}-1}}$的图象与性质.| x | … | -$\frac{9}{4}$ | -2 | -$\frac{7}{4}$ | -$\frac{3}{2}$ | -$\frac{5}{4}$ | … |
| y | … | 0.25 | 0.33 | 0.48 | 0.8 | 1.78 | … |
| x | -$\frac{3}{4}$ | -$\frac{1}{2}$ | $\frac{1}{4}$ | 0 | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{3}{4}$ |
| y | -2.29 | -1.33 | -1.07 | -1 | -1.07 | -1.33 | -2.29 |
| x | … | $\frac{5}{4}$ | $\frac{3}{2}$ | $\frac{7}{4}$ | 2 | $\frac{9}{4}$ | … |
| y | … | 1.78 | 0.8 | 0.48 | 0.33 | 0.25 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com