

分析 (1)观察统计图,先用A类的人数除以它所占的百分比得到总人数,再利用扇形统计图计算出C类人数,接着计算出D类人数,然后补全条形统计图;
(2)通过列表法展示所有12种等可能情况,再找出1人主持过班会而另一人没主持过班会的结果数,然后根据概率公式求解.
解答 解:(1)调查的学生总数为5÷10%=50(人),
C类人数为50×$\frac{108}{360}$=15(人),
D类人数为50-5-15-12=18(人),
条形统计图为: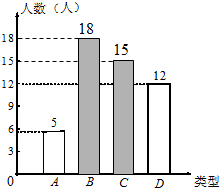
(2)设主持过班会的两人分别为A1、A2,另两人分别为B1、B2,填表如下:
结果 第二人 第一人 | A1 | A2 | B1 | B2 |
| A1 | (A1,A2) | (A1,B1) | (A1,B2) | |
| A2 | (A2,A1) | (A2,B1) | (A2,B2) | |
| B1 | (B1,A1) | (B1,A2) | (B1,B2) | |
| B2 | (B2,A1) | (B2,A2) | (B2,B1) |
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了统计图.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某供电公司,为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的图象如图所示.
某供电公司,为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
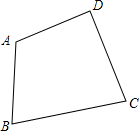 作图题:如图,西宁市沈那中学准备在校内一块四边形草坪内栽上一棵杏树,要求杏树的位置点P到边AB,BC的距离相等并且点P到A,D的距离也相等,请用尺规作图作出杏树的位置点P(用尺规作图法,保留作图痕迹,不写作法).
作图题:如图,西宁市沈那中学准备在校内一块四边形草坪内栽上一棵杏树,要求杏树的位置点P到边AB,BC的距离相等并且点P到A,D的距离也相等,请用尺规作图作出杏树的位置点P(用尺规作图法,保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com