
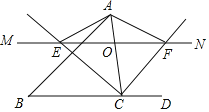
【题目】如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF,在下列结论中:①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.其中正确的是( )
A. ①④B. ①②C. ①②③D. ②③④
【答案】A
【解析】
①只要证明OC=OE,OC=OF即可.
②首先证明∠ECF=90°,若EC=CF,则∠OFC=45°,显然不可能,故②错误,
③利用勾股定理可得EF=13,推出OC=6.5,故③错误.
④根据矩形的判定方法即可证明.
∵MN∥CB,
∴∠OEC=∠BCE,∠OFC=∠ACF
∵∠ACE=∠BCE,∠ACF=∠DCF,
∴∠OEC=∠OCE,∠OFC=∠OCF,
∴OC=OE=OF,故①正确,
∵∠BCD=180°,
∴∠ECF=90°,
若EC=CF,则∠OFC=45°,显然不可能,故②错误,
∵∠ECF=90°,EC=12,CF=5,
∴EF=![]() =13,
=13,
∴OC=![]() EF=6.5,故③错误,
EF=6.5,故③错误,
∴OE=OF,OA=OC,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴四边形AECF是矩形.
故选:A.


科目:初中数学 来源: 题型:
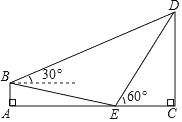
【题目】如图,斜坡BE,坡顶B到水平地面的距离AB为3米,坡底AE为18米,在B处,E处分别测得CD顶部点D的仰角为30°,60°,求CD的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
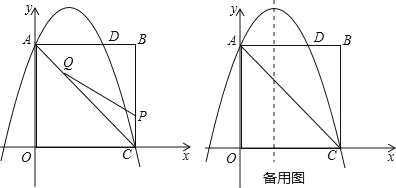
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
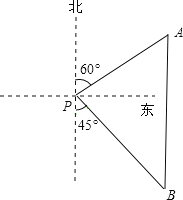
【题目】如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处.求此时渔船所在的B处与海洋观测站P的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
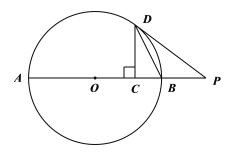
【题目】如图,点D在⊙O上,过点D的切线交直径AB的延长线于点P,DC⊥AB于点C.
(1)求证:DB平分∠PDC;
(2)如果DC = 6,![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
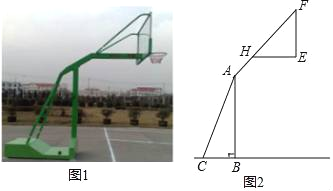
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长![]() 米,HF长
米,HF长![]() 米,HE长1米.
米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级共有6个班,要从中选出两个班代表学校参加一项重大活动,九(1)班是先进班,学校指定该班必须参加,另外再从九(2)班到九(6)班中选出一个班,九(4)班有同学建议用如下方法选班:从装有编号为1,2,3的三个白球的A袋中摸出一个球,再从装有编号也为1,2,3的三个红球的B袋中摸出一个球(两袋中球的大小、形状与质地完全一样),摸出的两个球编号之和是几就派几班参加.
(1)请用列表或画树形图的方法列举出摸出的两球编号的所有可能出现的结果;
(2)如果采用这一建议选班,对五个班是一样公平的吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,CD⊥AB,∠CAB的平分线AE交CD于点H、交CB于点E,EF⊥AB于点F,则下列结论中不正确的是( )
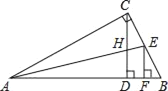
A. ∠ACD=∠BB. CH=CE=EFC. CH=HDD. AC=AF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com