
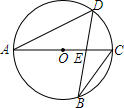
 如图,AC是⊙O的直径,AC=10,弦BD交AC于点E.
如图,AC是⊙O的直径,AC=10,弦BD交AC于点E.分析 (1)根据圆周角定理求出∠A=∠B,根据相似三角形的判定推出即可;
(2)连接CD,根据圆周角定理得到∠ADC=90°,根据垂径定理得到AC⊥BD,BE=DE,由射影定理得到DE2=BE2=AE.CE,∠AEC=∠BEC=90°,等量代换即可得到结论.
解答 证明:(1)∵弧CD=弧CD,
∴∠A=∠B,
又∵∠AED=∠BEC,
∴△ADE∽△BCE;
(2)连接CD,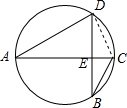
∵AC是⊙O的直径,
∴∠ADC=90°,
∵E是BD中点,AC是⊙的直径
∴AC⊥BD,BE=DE,
∴DE2=BE2=AE.CE,∠AEC=∠BEC=90°,
∴AD2+BC2=DE2+AE2+CE2+BE2=2DE2+AE2+CE2=AE2+CE2+2AE.CE=(AE+CE)2=100.
点评 本题考查了圆周角定理,相似三角形的判定,垂径定理,完全平方公式,射影定理,主要考查学生运用定理进行推理的能力,题目比较好,难度适中.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:选择题
 如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )
如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )| A. | 大于60° | B. | 小于60° | C. | 大于45° | D. | 小于45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.5m | B. | 0.8m | C. | 1m | D. | 1.2m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com