
 在平行四边形ABCD中,点E为AD中点,BE与AC相交于点O,则$\frac{{S}_{△AEO}}{{S}_{四边形DEOC}}$=$\frac{1}{5}$.
在平行四边形ABCD中,点E为AD中点,BE与AC相交于点O,则$\frac{{S}_{△AEO}}{{S}_{四边形DEOC}}$=$\frac{1}{5}$. 分析 根据平行四边形的性质得到AD=BC,AD∥BC,推出△AEO∽△BCO,根据相似三角形的性质得到$\frac{AE}{BC}=\frac{OE}{OB}$=$\frac{1}{2}$,得到S△ABO=2S△AOE,S△BCO=4S△AOE,于是得到S△ACB=6S△AOE,即可得到结论.
解答 解:在平行四边形ABCD中,
∵AD=BC,
∵点E为AD中点,
∴AE=$\frac{1}{2}$BC,
∵AD∥BC,
∴△AEO∽△BCO,
∴$\frac{AE}{BC}=\frac{OE}{OB}$=$\frac{1}{2}$,
∴$\frac{{S}_{△AOE}}{{S}_{△ABO}}$=$\frac{1}{2}$,
∴S△ABO=2S△AOE,
∵△AEO∽△BCO,
∴$\frac{{S}_{△AOE}}{{S}_{△BCO}}$=$\frac{1}{4}$,
∴S△BCO=4S△AOE,
∴S△ACB=6S△AOE,
∵S△ADC=S△ACB,
∴$\frac{{S}_{△AOE}}{{S}_{△ACD}}$=$\frac{1}{6}$,
∴$\frac{{S}_{△AEO}}{{S}_{四边形DEOC}}$=$\frac{1}{5}$,
故答案为:$\frac{1}{5}$.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,三角形的面积的计算,熟练掌握相似三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
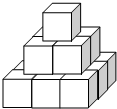 如图,把14个棱长为1cm的正方体木块,在地面上堆成如图所示的立体图形,然后向露出的表面部分喷漆,若1cm2需用漆2g,那么共需用漆84g.
如图,把14个棱长为1cm的正方体木块,在地面上堆成如图所示的立体图形,然后向露出的表面部分喷漆,若1cm2需用漆2g,那么共需用漆84g.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,AE是外角∠CAD的平分线,点F在AC上,连结BF并延长与AE交于点E.
如图,△ABC中,AB=AC,AE是外角∠CAD的平分线,点F在AC上,连结BF并延长与AE交于点E. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,过△ABC的顶点A分别作∠ACB及其外角的平分线的垂线,垂直分布为E、F,连接EF交AB于点M,交AC于点N,求证:
如图,过△ABC的顶点A分别作∠ACB及其外角的平分线的垂线,垂直分布为E、F,连接EF交AB于点M,交AC于点N,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点G处再测得自己的影长GH=4m,如果小明的身高为1.6m,GF=2m.求路灯杆AB的高度.
如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点G处再测得自己的影长GH=4m,如果小明的身高为1.6m,GF=2m.求路灯杆AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知平行四边形ABCD中,AB=2$\sqrt{5}$,AD=6,cot∠ABC=$\frac{1}{2}$,将边AB绕点A旋转,使得点B落在平行四边形ABCD的边上,其对应点为B′(点B′不与点B重合),那么sin∠CAB′=$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$.
如图,已知平行四边形ABCD中,AB=2$\sqrt{5}$,AD=6,cot∠ABC=$\frac{1}{2}$,将边AB绕点A旋转,使得点B落在平行四边形ABCD的边上,其对应点为B′(点B′不与点B重合),那么sin∠CAB′=$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,∠POA=60°求:
如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,∠POA=60°求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com