
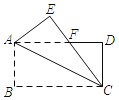
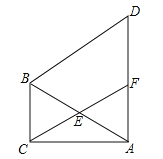
【题目】如图,在矩形ABCD中,AB=4,BC=8,把△ABC沿着AC向上翻折得到△AEC,EC交AD边于点F,则点F到AC的距离是_____.
【答案】![]()
【解析】
由矩形的性质可得AD=BC=8,AD∥BC,AB=CD=4,∠B=∠D=90°,由折叠的性质可得∠ACB=∠FCA,可证AF=CF,由勾股定理可求AF的长,由三角形的面积公式可求点F到AC的距离.
∵四边形ABCD是矩形,
∴AD=BC=8,AD∥BC,AB=CD=4,∠B=∠D=90°,
∴∠FAC=∠ACB,
∵把△ABC沿着AC向上翻折得到△AEC,
∴∠ACB=∠FCA,
∴∠FCA=∠FAC,
∴AF=CF,
∵AB=4,BC=8,
∴AC=![]() ,
,
在Rt△FDC中,CF2=CD2+DF2,
∴AF2=16+(8﹣AF)2,
∴AF=5
∵S△AFC=![]() ×AC×点F到AC的距离=
×AC×点F到AC的距离=![]() ×AF×CD=10
×AF×CD=10
∴点F到AC的距离=![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
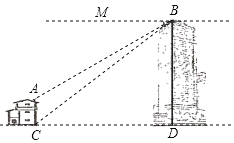
【题目】如图,两座建筑物的水平距离CD=60m,从点B测得点A的俯角∠MBA为30°,测得点C的俯角∠MBC为38°.求这两座建筑物的高度.参考数据:sin38°=0.62,cos38°≈0.79,tan38°=0.78,![]() ≈1.73,
≈1.73,![]() ≈1.41.
≈1.41.
查看答案和解析>>
科目:初中数学 来源: 题型:
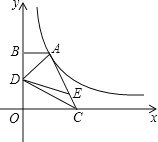
【题目】如图,点A在双曲线y=![]() (k≠0)的第一象限的分支上,AB垂直y轴于点B,点C在x轴正半轴上,OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,连接CD,若△CDE的面积为1,则k的值为_____.
(k≠0)的第一象限的分支上,AB垂直y轴于点B,点C在x轴正半轴上,OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,连接CD,若△CDE的面积为1,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=![]() ,OB=4,OE=1.
,OB=4,OE=1.
(1)求一次函数的解析式和反比例函数的解析式
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.

(1)求单摆的长度;
(2)求从点A摆动到点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,AD=4cm,EF经过对角线BD的中点O,分别交AD,BC于点E,F.
(1)求证:△BOF≌△DOE;
(2)当EF⊥BD时,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
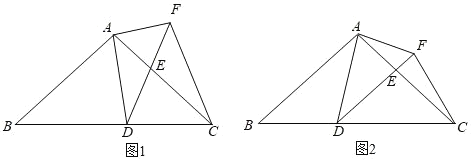
【题目】如图1,在△ABC中,AB=AC=10,BC=16,点D为BC边上的动点(点D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
(1)求证:△ABD∽△DCE;
(2)当DE∥AB时(如图2),求AE的长;
(3)点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com