
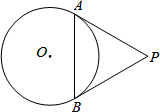
 如图,PA,PB分别与⊙O相切于点A,B,连接AB.∠APB=60°,AB=5,则PA的长是
如图,PA,PB分别与⊙O相切于点A,B,连接AB.∠APB=60°,AB=5,则PA的长是科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,学校要利用围墙建一长方形的自行车存车场,其它三面用护栏围起.其中与围墙平行的一边长(虚线部分为车场门)为(2m+3n)米(含门,门与其它护栏统一),与围墙垂直的边长比它少(m-n)米.
如图,学校要利用围墙建一长方形的自行车存车场,其它三面用护栏围起.其中与围墙平行的一边长(虚线部分为车场门)为(2m+3n)米(含门,门与其它护栏统一),与围墙垂直的边长比它少(m-n)米.查看答案和解析>>
科目:初中数学 来源: 题型:
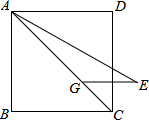 如图,正方形ABCD中,点G为对角线AC上一点,AG=AB.∠CAE=15°且AE=AC,连接GE.将线段AE绕点A逆时针旋转得到线段AF,使DF=GE,则∠CAF的度数为
如图,正方形ABCD中,点G为对角线AC上一点,AG=AB.∠CAE=15°且AE=AC,连接GE.将线段AE绕点A逆时针旋转得到线段AF,使DF=GE,则∠CAF的度数为查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
A、单项式-
| ||||||
| B、0和a都是代数式 | ||||||
C、数a的
| ||||||
| D、合并同类项-n2-n2=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com