
ЎҫМвДҝЎҝРЎГчҙъұнѧУІОјУЎ°ОТәНОТөДЧж№ъЎұЦчМвРыҙ«ҪМУэ»о¶ҜЈ¬ёГ»о¶Ҝ·ЦОӘБҪёцҪЧ¶ОЈ¬өЪТ»ҪЧ¶ОУРЎ°ёиЗъСЭіӘЎұЎўЎ°Кй·ЁХ№КҫЎұЎўЎ°ЖчАЦ¶АЧаЎұ3ёцПоДҝЈЁТАҙОУГ![]() Ўў
Ўў![]() Ўў
Ўў![]() ұнКҫЈ©Ј¬өЪ¶юҪЧ¶ОУРЎ°№ККВСЭҪІЎұЎўЎ°К«ёиАКЛРЎұ2ёцПоДҝЈЁТАҙОУГ
ұнКҫЈ©Ј¬өЪ¶юҪЧ¶ОУРЎ°№ККВСЭҪІЎұЎўЎ°К«ёиАКЛРЎұ2ёцПоДҝЈЁТАҙОУГ![]() Ўў
Ўў![]() ұнКҫЈ©Ј¬ІОјУИЛФұФЪГҝёцҪЧ¶ОёчЛж»ъійИЎТ»ёцПоДҝНкіЙ.
ұнКҫЈ©Ј¬ІОјУИЛФұФЪГҝёцҪЧ¶ОёчЛж»ъійИЎТ»ёцПоДҝНкіЙ.
ЈЁ1Ј©УГ»ӯКчЧҙНј»тБРұнөД·Ҫ·ЁЈ¬БРіцРЎГчІОјУПоДҝөДЛщУРөИҝЙДЬөДҪб№ыЈ»
ЈЁ2Ј©ЗуРЎГчЗЎәГійЦР![]() Ўў
Ўў![]() БҪёцПоДҝөДёЕВК.
БҪёцПоДҝөДёЕВК.

| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҝХјдИОТвСЎ¶ЁТ»өг![]() Ј¬ТФөг
Ј¬ТФөг![]() ОӘ¶ЛөгЈ¬ЧчИэМх»ҘПаҙ№ЦұөДЙдПЯ
ОӘ¶ЛөгЈ¬ЧчИэМх»ҘПаҙ№ЦұөДЙдПЯ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј®ХвИэМх»ҘПаҙ№ЦұөДЙдПЯ·ЦұріЖЧч
Ј®ХвИэМх»ҘПаҙ№ЦұөДЙдПЯ·ЦұріЖЧч![]() ЦбЎў
ЦбЎў![]() ЦбЎў
ЦбЎў![]() ЦбЈ¬НііЖОӘЧшұкЦбЈ¬ЛьГЗөД·ҪПт·ЦұрОӘ
ЦбЈ¬НііЖОӘЧшұкЦбЈ¬ЛьГЗөД·ҪПт·ЦұрОӘ![]() ЈЁЛ®ЖҪПтЗ°Ј©Ј¬
ЈЁЛ®ЖҪПтЗ°Ј©Ј¬![]() ЈЁЛ®ЖҪПтУТЈ©Ј¬
ЈЁЛ®ЖҪПтУТЈ©Ј¬![]() ЈЁКъЦұПтЙПЈ©·ҪПтЈ¬ХвСщөДЧшұкПөіЖОӘҝХјдЦұҪЗЧшұкПөЈ®Ҫ«ПаБЪИэёцГжөДГж»эјЗОӘ
ЈЁКъЦұПтЙПЈ©·ҪПтЈ¬ХвСщөДЧшұкПөіЖОӘҝХјдЦұҪЗЧшұкПөЈ®Ҫ«ПаБЪИэёцГжөДГж»эјЗОӘ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ЗТ
Ј¬ЗТ![]() өДРЎіӨ·ҪМеіЖОӘөҘО»іӨ·ҪМеЈ¬ПЦҪ«ИфёЙёцөҘО»іӨ·ҪМеФЪҝХјдЦұҪЗЧшұкПөДЪҪшРРВл·ЕЈ¬ТӘЗуВл·ЕКұҪ«өҘО»іӨ·ҪМе
өДРЎіӨ·ҪМеіЖОӘөҘО»іӨ·ҪМеЈ¬ПЦҪ«ИфёЙёцөҘО»іӨ·ҪМеФЪҝХјдЦұҪЗЧшұкПөДЪҪшРРВл·ЕЈ¬ТӘЗуВл·ЕКұҪ«өҘО»іӨ·ҪМе![]() ЛщФЪөДГжУл
ЛщФЪөДГжУл![]() Цбҙ№ЦұЈ¬
Цбҙ№ЦұЈ¬![]() ЛщФЪөДГжУл
ЛщФЪөДГжУл![]() Цбҙ№ЦұЈ¬
Цбҙ№ЦұЈ¬![]() ЛщФЪөДГжУл
ЛщФЪөДГжУл![]() Цбҙ№ЦұЈ¬ИзНј1ЛщКҫЈ®ИфҪ«
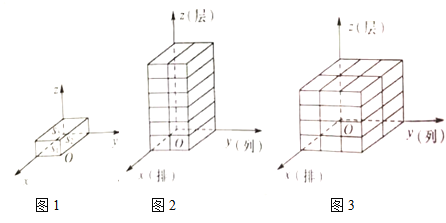
Цбҙ№ЦұЈ¬ИзНј1ЛщКҫЈ®ИфҪ«![]() Цб·ҪПтұнКҫөДБҝіЖОӘјёәОМеВл·ЕөДЕЕКэЈ¬
Цб·ҪПтұнКҫөДБҝіЖОӘјёәОМеВл·ЕөДЕЕКэЈ¬![]() Цб·ҪПтұнКҫөДБҝіЖОӘјёәОМеВл·ЕөДБРКэЈ¬¶юЦб·ҪПтұнКҫөДБҝіЖОӘјёәОМеВл·ЕөДІгКэЈ»ИзНј2КЗУЙИфёЙёцөҘО»іӨ·ҪМеФЪҝХјдЦұҪЗЧшұкДЪВл·ЕөДТ»ёцјёәОМеЈ¬ЖдЦРХвёцјёәОМе№ІВл·ЕБЛ
Цб·ҪПтұнКҫөДБҝіЖОӘјёәОМеВл·ЕөДБРКэЈ¬¶юЦб·ҪПтұнКҫөДБҝіЖОӘјёәОМеВл·ЕөДІгКэЈ»ИзНј2КЗУЙИфёЙёцөҘО»іӨ·ҪМеФЪҝХјдЦұҪЗЧшұкДЪВл·ЕөДТ»ёцјёәОМеЈ¬ЖдЦРХвёцјёәОМе№ІВл·ЕБЛ![]() ЕЕ
ЕЕ![]() БР
БР![]() ІгЈ¬УГУРРтКэЧйјЗЧч
ІгЈ¬УГУРРтКэЧйјЗЧч![]() Ј¬ИзНј3өДјёәОМеВл·ЕБЛ
Ј¬ИзНј3өДјёәОМеВл·ЕБЛ![]() ЕЕ
ЕЕ![]() БР
БР![]() ІгЈ¬УГУРРтКэЧйјЗЧч
ІгЈ¬УГУРРтКэЧйјЗЧч![]() Ј®ХвСщОТГЗҫНҝЙУГГҝТ»ёцУРРтКэЧй
Ј®ХвСщОТГЗҫНҝЙУГГҝТ»ёцУРРтКэЧй![]() ұнКҫТ»ЦЦјёәОМеөДВл·Е·ҪКҪЈ®
ұнКҫТ»ЦЦјёәОМеөДВл·Е·ҪКҪЈ®
ЈЁ1Ј©УРРтКэЧй![]() Лщ¶ФУҰөДВл·ЕөДјёәОМеКЗ______________Ј»
Лщ¶ФУҰөДВл·ЕөДјёәОМеКЗ______________Ј»
A.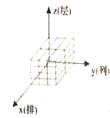 B.
B.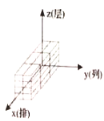 C.
C.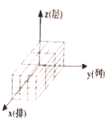 D.
D.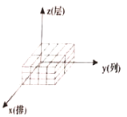
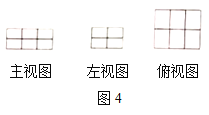
ЈЁ2Ј©Нј4КЗУЙИфёЙёцөҘО»іӨ·ҪМеВл·ЕөДТ»ёцјёәОМеөДИэКУНјЈ¬ФтХвЦЦВл·Е·ҪКҪөДУРРтКэЧйОӘЈЁ______Ј¬_______Ј¬_______Ј©Ј¬ЧйіЙХвёцјёәОМеөДөҘО»іӨ·ҪМеөДёцКэОӘ____________ёцЈ®
ЈЁ3Ј©ОӘБЛҪшТ»ІҪМҪҫҝУРРтКэЧй![]() өДјёәОМеөДұнГж»э№«КҪ
өДјёәОМеөДұнГж»э№«КҪ![]() Ј¬ДіН¬С§Хл¶ФИфёЙёцөҘО»іӨ·ҪМеҪшРРВл·ЕЈ¬ЦЖЧчБЛПВБРұнёсЈә
Ј¬ДіН¬С§Хл¶ФИфёЙёцөҘО»іӨ·ҪМеҪшРРВл·ЕЈ¬ЦЖЧчБЛПВБРұнёсЈә
јёәОМеУРРтКэЧй | өҘО»іӨ·ҪМеөДёцКэ | ұнГжЙПГж»эОӘS1өДёцКэ | ұнГжЙПГж»эОӘS2өДёцКэ | ұнГжЙПГж»эОӘS3өДёцКэ | ұнГж»э |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ёщҫЭТФЙП№жВЙЈ¬ЗлЦұҪУРҙіцУРРтКэЧй![]() өДјёәОМеұнГж»э
өДјёәОМеұнГж»э![]() өДјЖЛ㹫КҪЈ»ЈЁУГ
өДјЖЛ㹫КҪЈ»ЈЁУГ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ұнКҫЈ©
ұнКҫЈ©
ЈЁ4Ј©өұ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() КұЈ¬¶ФУЙ
КұЈ¬¶ФУЙ![]() ёцөҘО»іӨ·ҪМеВл·ЕөДјёәОМеҪшРРҙт°ьЈ¬ОӘБЛҪЪФјНв°ьЧ°ІДБПЈ¬ОТГЗҝЙТФ¶Ф
ёцөҘО»іӨ·ҪМеВл·ЕөДјёәОМеҪшРРҙт°ьЈ¬ОӘБЛҪЪФјНв°ьЧ°ІДБПЈ¬ОТГЗҝЙТФ¶Ф![]() ёцөҘО»іӨ·ҪМеВл·ЕөДјёәОМеұнГж»эЧоРЎөД№жВЙҪшРРМҪҫҝЈ¬ЗлДгёщҫЭЧФјәМҪҫҝөДҪб№ыЦұҪУРҙіцК№јёәОМеұнГж»эЧоРЎөДУРРтКэЧйЈ¬ХвёцУРРтКэЧйОӘЈЁ______Ј¬_______Ј¬ ______Ј©Ј¬ҙЛКұЗуіцөДХвёцјёәОМеұнГж»эөДҙуРЎОӘ____________ЈЁ·мП¶І»јЖЈ©
ёцөҘО»іӨ·ҪМеВл·ЕөДјёәОМеұнГж»эЧоРЎөД№жВЙҪшРРМҪҫҝЈ¬ЗлДгёщҫЭЧФјәМҪҫҝөДҪб№ыЦұҪУРҙіцК№јёәОМеұнГж»эЧоРЎөДУРРтКэЧйЈ¬ХвёцУРРтКэЧйОӘЈЁ______Ј¬_______Ј¬ ______Ј©Ј¬ҙЛКұЗуіцөДХвёцјёәОМеұнГж»эөДҙуРЎОӘ____________ЈЁ·мП¶І»јЖЈ©
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
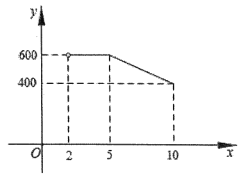
ЎҫМвДҝЎҝНшВзПъКЫКЗТ»ЦЦЦШТӘөДПъКЫ·ҪКҪ.ДіЕ©Гі№«ЛҫРВҝӘЙиБЛТ»јТНшөкЈ¬ПъКЫөұөШЕ©ІъЖ·.ЖдЦРТ»ЦЦөұөШМШІъФЪНшЙПКФПъКЫЈ¬ЖдіЙұҫОӘГҝЗ§ҝЛ2ФӘ.№«ЛҫФЪКФПъКЫЖЪјдЈ¬өчІй·ўПЦЈ¬ГҝМмПъКЫБҝ![]() УлПъКЫөҘјЫ
УлПъКЫөҘјЫ![]() ЈЁФӘЈ©ВъЧгИзНјЛщКҫөДәҜКэ№ШПөЈЁЖдЦР
ЈЁФӘЈ©ВъЧгИзНјЛщКҫөДәҜКэ№ШПөЈЁЖдЦР![]() Ј©.
Ј©.
ЈЁ1Ј©Иф![]() Ј¬Зу
Ј¬Зу![]() Ул
Ул![]() Ц®јдөДәҜКэ№ШПөКҪЈ»
Ц®јдөДәҜКэ№ШПөКҪЈ»
ЈЁ2Ј©ПъКЫөҘјЫ![]() ОӘ¶аЙЩФӘКұЈ¬ГҝМмөДПъКЫАыИуЧоҙуЈҝЧоҙуАыИуКЗ¶аЙЩФӘЈҝ
ОӘ¶аЙЩФӘКұЈ¬ГҝМмөДПъКЫАыИуЧоҙуЈҝЧоҙуАыИуКЗ¶аЙЩФӘЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘУӯҪУЎ°КАҪз»ӘИЛСЧөЫ№КАпС°ёщҪЪЎұЈ¬Ді№Өі§ҪУөҪТ»ЕъјНДоЖ·ЙъІъ¶©өҘЈ¬°ҙТӘЗуФЪ15МмДЪНкіЙЈ¬Фј¶ЁХвЕъјНДоЖ·өДіці§јЫОӘГҝјю20ФӘЈ¬ЙиөЪxМмЈЁ1ЎЬxЎЬ15Ј¬ЗТxОӘХыКэЈ©ГҝјюІъЖ·өДіЙұҫКЗpФӘЈ¬pУлxЦ®јд·ыәПТ»ҙОәҜКэ№ШПөЈ¬Іҝ·ЦКэҫЭИзұнЈә
МмКэЈЁxЈ© | 1 | 3 | 6 | 10 |
ГҝјюіЙұҫpЈЁФӘЈ© | 7.5 | 8.5 | 10 | 12 |
ИООсНкіЙәуЈ¬НіјЖ·ўПЦ№ӨИЛАоКҰёөөЪxМмЙъІъөДІъЖ·јюКэyЈЁјюЈ©УлxЈЁМмЈ©ВъЧгИзПВ№ШПөЈәy=![]() Ј¬
Ј¬
ЙиАоКҰёөөЪxМмҙҙФмөДІъЖ·АыИуОӘWФӘЈ®
ЈЁ1Ј©ЦұҪУРҙіцpУлxЈ¬WУлxЦ®јдөДәҜКэ№ШПөКҪЈ¬ІўЧўГчЧФұдБҝxөДИЎЦө·¶О§Јә
ЈЁ2Ј©ЗуАоКҰёөөЪјёМмҙҙФмөДАыИуЧоҙуЈҝЧоҙуАыИуКЗ¶аЙЩФӘЈҝ
ЈЁ3Ј©ИООсНкіЙәуЈ®НіјЖ·ўПЦЖҪҫщГҝёц№ӨИЛГҝМмҙҙФмөДАыИуОӘ299ФӘЈ®№Өі§ЦЖ¶ЁИзПВҪұАшЦЖ¶ИЈәИз№ыТ»ёц№ӨИЛДіМмҙҙФмөДАыИ󳬹эёГЖҪҫщЦөЈ¬ФтёГ№ӨИЛөұМмҝЙ»сөГ20ФӘҪұҪрЈ®ЗлјЖЛгАоКҰёө№ІҝЙ»сөГ¶аЙЩФӘҪұҪрЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЖҪРРЛДұЯРО![]() өД¶ФҪЗПЯПаҪ»УЪөг
өД¶ФҪЗПЯПаҪ»УЪөг![]() Ј¬
Ј¬![]() өДНвҪУФІҪ»
өДНвҪУФІҪ»![]() УЪөг
УЪөг![]() ЗТФІРД
ЗТФІРД![]() ЗЎәГВдФЪ
ЗЎәГВдФЪ![]() ұЯЙПЈ¬Б¬ҪУ
ұЯЙПЈ¬Б¬ҪУ![]() Ј¬Иф
Ј¬Иф![]() .
.
ЈЁ1Ј©ЗуЦӨЈә![]() ОӘ
ОӘ![]() ЗРПЯ.
ЗРПЯ.
ЈЁ2Ј©Зу![]() өД¶ИКэ.
өД¶ИКэ.
ЈЁ3Ј©Иф![]() өД°лҫ¶ОӘ1Ј¬Зу
өД°лҫ¶ОӘ1Ј¬Зу![]() өДіӨ.
өДіӨ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҙУ©Ғ4Ј¬©Ғ3Ј¬©Ғ2Ј¬©Ғ1Ј¬0Ј¬1Ј¬3Ј¬4Ј¬5ХвҫЕёцКэЦРЈ¬Лж»ъійИЎТ»ёцКэЈ¬јЗОӘaЈ¬ФтКэaК№№ШУЪxөДІ»өИКҪЧй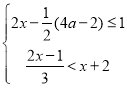 ЦБЙЩУРЛДёцХыКэҪвЈ¬ЗТ№ШУЪxөД·ЦКҪ·ҪіМ
ЦБЙЩУРЛДёцХыКэҪвЈ¬ЗТ№ШУЪxөД·ЦКҪ·ҪіМ![]() ЈҪ1УР·ЗёәХыКэҪвөДёЕВККЗЈЁЎЎЎЎЈ©
ЈҪ1УР·ЗёәХыКэҪвөДёЕВККЗЈЁЎЎЎЎЈ©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
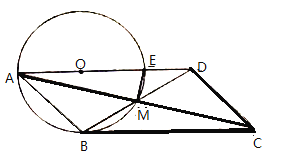
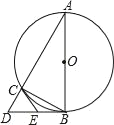
ЎҫМвДҝЎҝИзНјЈ¬ТФЎчABCөДұЯABОӘЦұҫ¶ЧчЎСOЈ¬ЗТ¶ҘөгCФЪЎСOЙПЈ¬№эөгBөДЗРПЯУлACөДСУіӨПЯҪ»УЪөгDЈ¬EКЗBDЦРөгЈ¬Б¬ҪУCEЈ®
ЈЁ1Ј©ЗуЦӨЈәCEКЗЎСOөДЗРПЯЈ»
ЈЁ2Ј©ИфACЈҪ8Ј¬BCЈҪ6Ј¬ЗуBDәНCEөДіӨЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЈәХэ·ҪРОABCDЦРЈ¬ЎПMAN=45ЎгЈ¬ЎПMANИЖөгAЛіКұХлРэЧӘЈ¬ЛьөДБҪұЯ·ЦұрҪ»CBЈ¬DCЎўDCЈЁ»тЛьГЗөДСУіӨПЯЈ©УЪөгMЈ¬N.

ЈЁ1Ј©өұЎПMANИЖөгAРэЧӘөҪЈЁИзНј1Ј©КұЈ¬ЗуЦӨЈәBM+DN=MNЈ»
ЈЁ2Ј©өұЎПMANИЖөгAРэЧӘөҪИзНј2өДО»ЦГКұЈ¬ІВПлПЯ¶ОBMЈ¬DNәНMNЦ®јдУЦУРФхСщөДКэБҝ№ШПөДШЈҝЗлЦұҪУРҙіцДгөДІВПлЎЈЈЁІ»РиТӘЦӨГчЈ©
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЈәABКЗЎСOөДЦұҫ¶Ј¬BDКЗЎСOөДПТЈ¬СУіӨBDөҪөгCЈ¬К№ABЈҪACЈ¬Б¬ҪУACЈ¬№эөгDЧчDEЎНACЈ¬ҙ№ЧгОӘ EЈ®
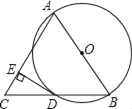
ЈЁ1Ј©ЗуЦӨЈәDCЈҪBDЈ»
ЈЁ2Ј©ЗуЦӨЈәDEОӘЎСOөДЗРПЯЈ»
ЈЁ3Ј©ИфABЈҪ12Ј¬ADЈҪ6![]() Ј¬Б¬ҪУODЈ¬ЗуЙИРОBODөДГж»эЈ®
Ј¬Б¬ҪУODЈ¬ЗуЙИРОBODөДГж»эЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com