
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC、DC(或它们的延长线)于点M,N.

(1)当∠MAN绕点A旋转到(如图1)时,求证:BM+DN=MN;
(2)当∠MAN绕点A旋转到如图2的位置时,猜想线段BM,DN和MN之间又有怎样的数量关系呢?请直接写出你的猜想。(不需要证明)
【答案】(1)见解析;(2)DN-BM=MN
【解析】
(1)根据题意延长CB至E使得BE=DN,连接AE,利用全等三角形判定证明△ABE≌△AND和△EAM≌△NAM,等量代换即可求证BM+DN=MN;
(2)由题意在DN上截取DE=MB,连接AE,证△ABM≌△ADE,推出AM=AE;∠MAB=∠EAD,求出∠EAN=∠MAN,根据SAS证△AMN≌△AEN,推出MN=EN即可.
解:(1)证明:如图1,延长CB至E使得BE=DN,连接AE,
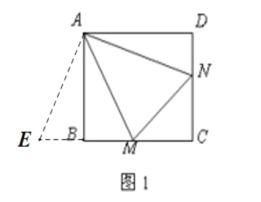
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABC=90°=∠ABE,
在△ADN和△ABE中
∵AD=AB∠D=∠ABEDN=BE,
△ABE≌△ADN(SAS),
∴∠BAE=∠DAN,AE=AN,
∴∠EAN=∠BAE+∠BAN=∠DAN+∠BAN=90°,
∵∠MAN=45°,
∴∠EAM=∠MAN,
∵在△EAM和△NAM中
AE=AN∠EAM=∠NAMAM=AM,
∴△EAM≌△NAM,
∴MN=ME,
∵ME=BM+BE=BM+DN,
∴BM+DN=MN;
(2)猜想:线段BM,DN和MN之间的等量关系为:DN-BM=MN.
证明:如图2,在DN上截取DE=MB,连接AE,
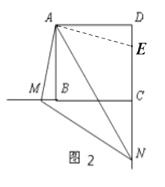
∵AD=AB,∠D=∠ABM=90°,BM=DE,
∴△ABM≌△ADE(SAS).
∴AM=AE;∠MAB=∠EAD,
∵∠MAN=45°=∠MAB+∠BAN,
∴∠DAE+∠BAN=45°,
∴∠EAN=90°-45°=45°=∠MAN,
∵在△AMN和△AEN中,AM=AE,∠MAN=∠EAN,AN=AN,
∴△AMN≌△AEN(SAS),
∴MN=EN,
∵DN-DE=EN,
∴DN-BM=MN.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴正半轴上,点
轴正半轴上,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 、点
、点![]() 重合),连结
重合),连结![]() 、
、![]() ,过点
,过点![]() 作射线
作射线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 边于点
边于点![]() ,且
,且![]() ,令
,令![]() ,
,![]() .
.

(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)在点![]() 的运动过程中,是否存在
的运动过程中,是否存在![]() ,使
,使![]() 的面积与
的面积与![]() 的面积之和等于
的面积之和等于![]() 的面积.若存在,请求
的面积.若存在,请求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明代表学校参加“我和我的祖国”主题宣传教育活动,该活动分为两个阶段,第一阶段有“歌曲演唱”、“书法展示”、“器乐独奏”3个项目(依次用![]() 、
、![]() 、
、![]() 表示),第二阶段有“故事演讲”、“诗歌朗诵”2个项目(依次用
表示),第二阶段有“故事演讲”、“诗歌朗诵”2个项目(依次用![]() 、
、![]() 表示),参加人员在每个阶段各随机抽取一个项目完成.
表示),参加人员在每个阶段各随机抽取一个项目完成.
(1)用画树状图或列表的方法,列出小明参加项目的所有等可能的结果;
(2)求小明恰好抽中![]() 、
、![]() 两个项目的概率.
两个项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为( )

A.![]() B.0C.
B.0C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
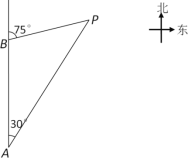
【题目】如图,海南省三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(结果精确到0.1海里,参考数据:tan75°≈3.732,sin75°≈0.966,sin15°≈0.259,![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙P的圆心为P(﹣3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.
(1)在图中作出⊙P关于y轴对称的⊙P′.根据作图直接写出⊙P′与直线MN的位置关系.
(2)若点N在(1)中的⊙P′上,求PN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com