
| A. | a•a3=a3 | B. | a4+a3=a2 | C. | (a2)5=a7 | D. | (-ab)2=a2b2 |
分析 A:根据同底数幂的乘法法则判断即可.
B:根据合并同类项的方法判断即可.
C:根据幂的乘方的运算方法判断即可.
D:根据积的乘方的运算方法判断即可.
解答 解:∵a•a3=a4,
∴选项A不正确;
∵a4+a3≠a2,
∴选项B不正确;
∵(a2)5=a10,
∴选项C不正确;
∵(-ab)2=a2b2,
∴选项D正确.
故选:D.
点评 (1)此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).
(2)此题还考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:①底数必须相同;②按照运算性质,只有相乘时才是底数不变,指数相加.
(3)此题还考查了合并同类项的方法,要熟练掌握.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
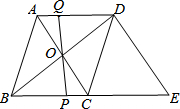 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,P为线段BC上一点(除端点外),连接PO并延长交AD于点Q,延长BC到点E,使CE=BC,连接DE.
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,P为线段BC上一点(除端点外),连接PO并延长交AD于点Q,延长BC到点E,使CE=BC,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
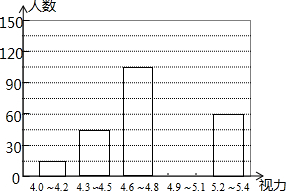 为进一步加强中小学生近视眼的防控工作,市教育局近期下发了有关文件,将学生视力保护工作纳入学校和教师的考核内容,为此,某县教育部门对今年初中毕业生的视力进行一次抽样调查,并根据调查结果绘制如下频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
为进一步加强中小学生近视眼的防控工作,市教育局近期下发了有关文件,将学生视力保护工作纳入学校和教师的考核内容,为此,某县教育部门对今年初中毕业生的视力进行一次抽样调查,并根据调查结果绘制如下频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:| 视力 | 频数(人) |
| 4.0~4.2 | 15 |
| 4.3~4.5 | 45 |
| 4.6~4.8 | 105 |
| 4.9~5.1 | a |
| 5.2~5.4 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )| A. | $\frac{1}{2}$π-1 | B. | $\frac{1}{2}$π-2 | C. | π-2 | D. | π-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
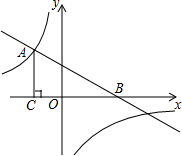 如图,一次函数y=-$\frac{1}{2}$x+2的图象与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象的交点为A(-2,3).
如图,一次函数y=-$\frac{1}{2}$x+2的图象与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象的交点为A(-2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
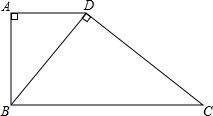 已知,如图,梯形ABCD中,AD∥BC,∠A=90°,BC=10,CD=8,对角线BD⊥CD.
已知,如图,梯形ABCD中,AD∥BC,∠A=90°,BC=10,CD=8,对角线BD⊥CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com