
【题目】如图,在 Rt△ABC 中,∠ACB=90°,AC=6cm,∠ABC=30°,动点 P 从点 B 出发,在 BA 边上以每秒 2cm 的速度向点 A 匀速运动,同时动点 Q 从点 C 出发,在 CB 边上以每秒![]() cm 的速度向点 B 匀速运动,运动时间为 t 秒(0≤t≤6),连接 PQ,以 PQ 为直径作⊙O.
cm 的速度向点 B 匀速运动,运动时间为 t 秒(0≤t≤6),连接 PQ,以 PQ 为直径作⊙O.
(1)当 t=1 时,求△BPQ 的面积;
(2)设⊙O 的面积为 y,求 y 与 t 的函数解析式;
(3)若⊙O 与 Rt△ABC 的一条边相切,求 t 的值.

【答案】(1)![]() ;(2)y=
;(2)y=![]() t2-18πt+27π;(3)t 的值为 3 或
t2-18πt+27π;(3)t 的值为 3 或![]() 或 0 或
或 0 或![]() .
.
【解析】
(1)连接DP,根据△BPM~△BAC,可得PD=t,BQ=![]() (6-t),然后得到
(6-t),然后得到
![]() =
=![]() BQ·PD即可得出结论;
BQ·PD即可得出结论;
(2)先表示出DP,BD,进而利用勾股定理求出PQ的平方,最后用圆的面积公式即可得出结论;
(3)分![]() O与BC相切、
O与BC相切、![]() O与AB相切,
O与AB相切, ![]() O与AC相切时,三种情况分类讨论即可得出结论.
O与AC相切时,三种情况分类讨论即可得出结论.
解:
(1)如图 1,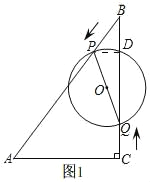
在 Rt△ABC 中,∠ABC=30°,AC=6,
∴AB=12,BC=6![]() ,
,
由运动知,BP=2t,CQ=![]() t,
t,
∴BQ=BC﹣CQ=![]() (6﹣t),连接 DP,
(6﹣t),连接 DP,
∵PQ 是⊙O 的直径,
∴∠PDQ=90°
∵∠C=90°,
∴PD∥AC.
∴△BPD∽△BAC,
∴![]() =
=![]()
∴![]() =
=![]() ,
,
∴DP=t,BD= ![]() t,
t,
![]() =
= ![]() BQPD=
BQPD= ![]() ×(6﹣t)t=﹣
×(6﹣t)t=﹣![]() t
t![]() +3
+3![]() t
t
∴当 t=1 时,![]() =
=![]() ﹣
﹣![]() +3
+3![]() =
=![]() ;
;
(2)DQ=|BQ﹣BD|=| ![]() (6﹣t)﹣
(6﹣t)﹣ ![]() t|=2
t|=2![]() |3﹣t|,PQ
|3﹣t|,PQ![]() =PD
=PD![]() +DQ
+DQ![]() =t
=t![]() +[2
+[2![]()
(3﹣t)]![]() =13t
=13t![]() ﹣72t+108,
﹣72t+108,
∴y=π×(![]() )
)![]() =
= ![]() t
t![]() ﹣18πt+27π,
﹣18πt+27π,
(3)由运动知,BP=2t,CQ=![]() t,
t,
∴BQ=BC﹣CQ=![]() (6﹣t),当⊙O 与 BC 相切时,PQ⊥BC,
(6﹣t),当⊙O 与 BC 相切时,PQ⊥BC,
∴△BPQ∽△BAC,
∴![]()
∴![]()
∴![]() =3,
=3,
当⊙O 与 AB 相切时,PQ⊥AB,
∴△BPQ∽△BCA
∴![]()
∴![]() ,
,
∴![]() =
= ![]() ,
,
当⊙O 与 AC 相切时,
如图 2 ,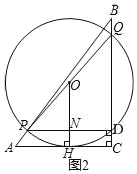
过点 O 作 OH⊥AC 于点 H,交 PD 于点 N,
∴OH∥BC,
∵点 O 是 PQ 的中点,
∴ON= ![]() QD,
QD,
由(1)知,BQ=![]() (6﹣t),BD=
(6﹣t),BD=![]() t,
t,
∴QD=BD﹣BQ=2![]() (t﹣3),DC=BC﹣BD=6
(t﹣3),DC=BC﹣BD=6![]() ﹣
﹣![]() t=
t=![]() (6﹣t)
(6﹣t)
∴OH=ON+NH= ![]() QD+DC=
QD+DC= ![]() ×2 (t﹣3)+ (6﹣t)=3 ,
×2 (t﹣3)+ (6﹣t)=3 ,
∴PQ=2OH=6![]() ,
,
由(2)知,PQ![]() =13t
=13t![]() ﹣72t+108
﹣72t+108
∴13t![]() ﹣72t+108=36×3解得
﹣72t+108=36×3解得 ![]() =0,
=0,![]() =
=![]() ,
,
综上所述,若⊙O 与 Rt△ABC 的一条边相切,t 的值为 3 或![]() 或 0 或
或 0 或![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为( )
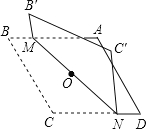
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.了解飞行员视力的达标率应使用抽样调查
B.一组数据3,6,6,7,9的中位数是6
C.从2000名学生中选200名学生进行抽样调查,样本容量为2000
D.一组数据1,2,3,4,5的方差是10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一只不透明的布袋中装有红球 3 个、黄球 1 个,这些球除颜色外都相同,均匀摇匀.
(1)从布袋中一次摸出 1 个球,计算“摸出的球恰是黄球”的概率;
(2)从布袋中一次摸出 2 个球,计算“摸出的球恰是一红一黄”的概率(用“ 画树状图”或“列表”的方法写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y=![]() (x>0)的图象过点A.
(x>0)的图象过点A.
(1)求直线l和反比例函数的解析式;
(2)在函数y=![]() (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
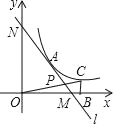
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com