
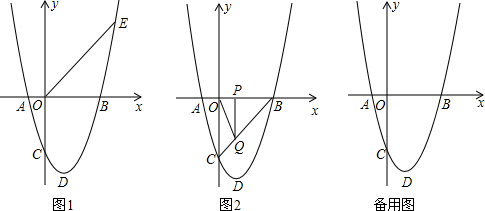
ЗжЮі ЃЈ1ЃЉЧѓГіEЕузјБъЃЌНјЖјПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЯШИљОнЬтвтХаЖЯГіЁїBPQЪЧжБНЧШ§НЧаЮЃЌдйгЩШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШЧѓГіжБЯпANЕФНтЮіЪНЃЌдйгУmБэЪОГіЕуMЃЌM1ЃЌM2ЕФзјБъЃЌЗжM1M22=M1D2+M2D2ЃЌM1D2=M1M22+M2D2МАM2D2=M1M22+M1D2Ш§жжЧщПіНјааЬжТлЃЎ
НтД№ НтЃКЃЈ1ЃЉЁпСюx=$\frac{3+\sqrt{21}}{2}$ЃЌдђy=$\frac{3+\sqrt{21}}{2}$ЃЌ
ЁрЁЯBOE=45ЁуЃЌ
ЁрЁЯAOE=180Ёу-45Ёу=135ЁуЃЛ
ЃЈ2ЃЉЁпBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ-3ЃЉ
ЁрЁїOBCЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁпЖЏЕуPдкЯпЖЮOBЩЯвдУПУы1ИіЕЅЮЛГЄЕФЫйЖШДгOЕуГіЗЂЯђBЕудЫЖЏЃЌЭЌЪБЖЏЕуQдкЯпЖЮBCЩЯвдУПУы$\sqrt{2}$ИіЕЅЮЛГЄЖШЕФЫйЖШДгCЕуГіЗЂЯђBЕудЫЖЏЃЌ
ЁрЁїBPQЪЧжБНЧШ§НЧаЮЃЌ
ЁрS=$\frac{1}{2}$tЃЈ3-tЃЉЃЌ
ЁрХзЮяЯпЕФЖдГЦжсЮЊt=$\frac{3}{2}$ЃЌ
ЁрЕБt=$\frac{3}{2}$ЪБЃЌSзюДѓ=$\frac{9}{8}$ЃЛ
ЃЈ3ЃЉЁпn=$\frac{3}{2}$ЃЌ
Ёрy=ЃЈ$\frac{3}{2}$ЃЉ2-2ЁС$\frac{3}{2}$-3=-$\frac{15}{4}$ЃЌ
ЁрNЃЈ$\frac{3}{2}$ЃЌ-$\frac{15}{4}$ЃЉЃЎ
ЁпAЃЈ-1ЃЌ0ЃЉЃЌ
ЁржБЯпANЕФНтЮіЪНЮЊy=-$\frac{3}{2}$x-$\frac{3}{2}$ЃЎ
ЩшMЃЈmЃЌ-$\frac{3}{2}$m-$\frac{3}{2}$ЃЉЃЌдђM1ЃЈmЃЌ$\frac{3}{2}$m+$\frac{3}{2}$ЃЉЃЌM2ЃЈ-mЃЌ-$\frac{3}{2}$m-$\frac{3}{2}$ЃЉЃЎ
ЁпDЃЈ1ЃЌ-4ЃЉЃЌ
ЁрM1M22=ЃЈ2mЃЉ2+ЃЈ3m+3ЃЉ2=13m2+18m+9ЃЌ
M1D2=ЃЈm-1ЃЉ2+ЃЈ$\frac{3}{2}$m+$\frac{11}{2}$ЃЉ2=$\frac{13}{4}$m2+$\frac{29}{2}$m+$\frac{125}{4}$ЃЎ
M2D2=ЃЈm+1ЃЉ2+ЃЈ$\frac{3}{2}$m-$\frac{5}{2}$ЃЉ2=$\frac{13}{4}$m2-$\frac{11}{2}$m+$\frac{29}{4}$ЃЎ
ЂйЁпЕБM1M22=M1D2+M2D2ЃЌМД13m2+18m+9=$\frac{13}{2}$m2+9m+$\frac{77}{2}$ЃЌ
Ёрm=$\frac{-8ЁР8\sqrt{53}}{26}$=$\frac{-9ЁР4\sqrt{53}}{13}$ЃЌ
Ёр-$\frac{3}{2}$ЃЈm+1ЃЉ=-$\frac{3}{2}$•$\frac{4ЁР4\sqrt{53}}{13}$=$\frac{6ЁР6\sqrt{53}}{13}$ЃЌ
ЁрMЃЈ$\frac{-9+4\sqrt{53}}{13}$ЃЌ-$\frac{6+6\sqrt{53}}{13}$ЃЉЛђMЃЈ$\frac{-9-4\sqrt{53}}{13}$ЃЌ-$\frac{6-6\sqrt{53}}{13}$ЃЉЃЛ
ЂкЕБM1D2=M1M22+M2D2ЃЌМД$\frac{13}{4}$m2+$\frac{29}{2}$m+$\frac{125}{4}$=13m2+18m+9+$\frac{13}{4}$m2-$\frac{11}{2}$m+$\frac{29}{4}$ЃЌ
ећРэЕУЃК13m2-2m-15=0ЃЌНтЕУm=$\frac{15}{13}$Лђm=-1ЃЌ
ЁрMЃЈ$\frac{15}{13}$ЃЌ-$\frac{42}{13}$ЃЉЛђMЃЈ-1ЃЌ0ЃЉЃЛ
ЂлЕБM2D2=M1M22+M1D2ЃЌМД$\frac{13}{4}$m2-$\frac{11}{2}$m+$\frac{29}{4}$=13m2+18m+9+$\frac{13}{4}$m2+$\frac{29}{2}$m+$\frac{125}{4}$ЃЌ
Ёр13m2+38m+33=0ЃЌ
ЁрЁї=382-4ЁС13ЁС33=1444-1716ЃМ0ЃЌ
ЁрДЫжжЧщПіВЛДцдкЃЎ
злЩЯЫљЪОЃЌMЃЈ$\frac{-9+4\sqrt{53}}{13}$ЃЌ-$\frac{6+6\sqrt{53}}{13}$ЃЉЛђMЃЈ$\frac{-9-4\sqrt{53}}{13}$ЃЌ-$\frac{6-6\sqrt{53}}{13}$ЃЉЛђMЃЈ$\frac{15}{13}$ЃЌ-$\frac{42}{13}$ЃЉЛђMЃЈ-1ЃЌ0ЃЉЃЎ
ЕуЦР БОЬтПМЕФВщЪЧЖўДЮКЏЪ§злКЯЬтЃЌЩцМАЕНХзЮяЯпЩЯЕуЕФзјБъЬиЕуЁЂШ§НЧаЮЕФаджЪМАЙДЙЩЖЈРэЕШжЊЪЖЃЌФбЖШНЯДѓЃЌдкНтД№ЃЈ3ЃЉЪБвЊзЂвтНјааЗжРрЬжТлЃЎ


 УћаЃСЗПМОэЦкФЉГхДЬОэЯЕСаД№АИ
УћаЃСЗПМОэЦкФЉГхДЬОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ББЦЋЖЋ42Ёу | BЃЎ | ББЦЋЖЋ48Ёу | CЃЎ | ФЯЦЋЮї48Ёу | DЃЎ | ЖЋББЗНЯђ.. |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 1Иі | BЃЎ | 2Иі | CЃЎ | 3Иі | DЃЎ | 4Иі |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
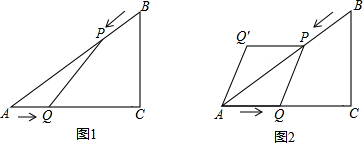
 ШчЭМЃЌ?ABCDЕФЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌЁїOABЪЧЕШБпШ§НЧаЮЃЌЧвAB=4ЃЌ
ШчЭМЃЌ?ABCDЕФЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌЁїOABЪЧЕШБпШ§НЧаЮЃЌЧвAB=4ЃЌВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
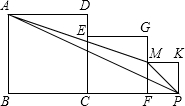 ШчЭМЫљЪОЃЌШ§Иіе§ЗНаЮБпГЄЗжБ№ЮЊ1ЃЌ2ЃЌ3ЃЌЧѓШ§НЧаЮAMPЕФУцЛ§ЃЎ
ШчЭМЫљЪОЃЌШ§Иіе§ЗНаЮБпГЄЗжБ№ЮЊ1ЃЌ2ЃЌ3ЃЌЧѓШ§НЧаЮAMPЕФУцЛ§ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com